Giải phương trình đồng dư sau:
7x4 -8x-2=0 (mod27)
1/ Chứng minh phương trình vô nghiệm:
a) \(-16x^2-8x+4=0\)
b) \(-x^2+4x-4=0\)
2/ Giải phương trình sau:
\(\left(x^2-2x-4\right)\left(2x^2-8x-1\right)=0\)
Bài 1:
b: \(\Leftrightarrow x-2=0\)
hay x=2
Giải phương trình sau:
\(2x\left(8x+1\right)\left(8x^2-x+2\right)-126=0\)
Sửa đề: 8x-1
=>2(8x^2-x)(8x^2-x+2)-126=0
=>2[(8x^2-x)^2+2(8x^2-x)]-126=0
=>(8x^2-x)^2+2(8x^2-x)-63=0
=>(8x^2-x+9)(8x^2-x-7)=0
=>8x^2-x-7=0
=>x=1 hoặc x=-7/8
Giải các phương trình mũ sau: - 8 x + 2 . 4 x + 2 x - 2 = 0
Đặt t = 2 x (t > 0), ta có phương trình:
− t 3 + 2 t 2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
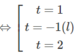
Do đó: 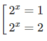
Giải bất phương trình sau:
x2 - 8x - 9 ≥ 0
x2 - 8x - 9 ≥ 0
<=> (x+1)(x-9)\(\ge\)0
<=> \(\hept{\begin{cases}x+1\ge0\\x-9\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}x+1\le0\\x-9\le0\end{cases}}\)
<=> \(\orbr{\begin{cases}x\ge9\\x\le-1\end{cases}}\)
Giải các phương trình sau:
a) x + 3 3 − x − 1 3 = 0 ;
b) x 4 + x 2 − 2 = 0 ;
c) x 3 + 3 x 2 + 6 x + 4 = 0 ;
d) x 3 − 6 x 2 + 8 x = 0 .
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
Giải phương trình sau :
\(3x^3-8x^2-2x+4=0\)
\(\Leftrightarrow3x^3-2x^2-6x^2+4x-6x+4=0\)
\(\Leftrightarrow x^2\left(3x-2\right)-2x\left(3x-2\right)-2\left(3x-2\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow x=\frac{2}{3}\)
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
Giải phương trình sau:
a) (x^2+x+1)*(6-2x)+0
b) (8x-4)*(x^2+2x+2)+0
Đề bài sai ! Sửa ạ :
a) \(\left(x^2+x+1\right)\left(6-2x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+x+1=0\\6-2x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+\frac{1}{2}\right)^2+\frac{3}{4}=0\left(ktm\right)\\x=3\left(tm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{3\right\}\)
b) \(\left(8x-4\right)\left(x^2+2x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}8x-4=0\\x^2+2x+2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\left(tm\right)\\\left(x+1\right)^2+1=0\left(ktm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{2}\right\}\)
\(\left(x^2+x+1\right)\left(6-2x\right)=0\)
Mà \(x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{1}{4}>0\)
\(\Rightarrow6-2x=0\Rightarrow x=3\)
1.Tìm giá trị nhỏ nhất của biểu thức sau:
A= |8x-7|+|8x-2|+2009
2. Chứng minh phương trình
2mx-5=-x+6m-2 luôn có 1 nghiệm x không phụ thuộc vào m
3 Giải phương trình
x3-5x2+8x-4=0