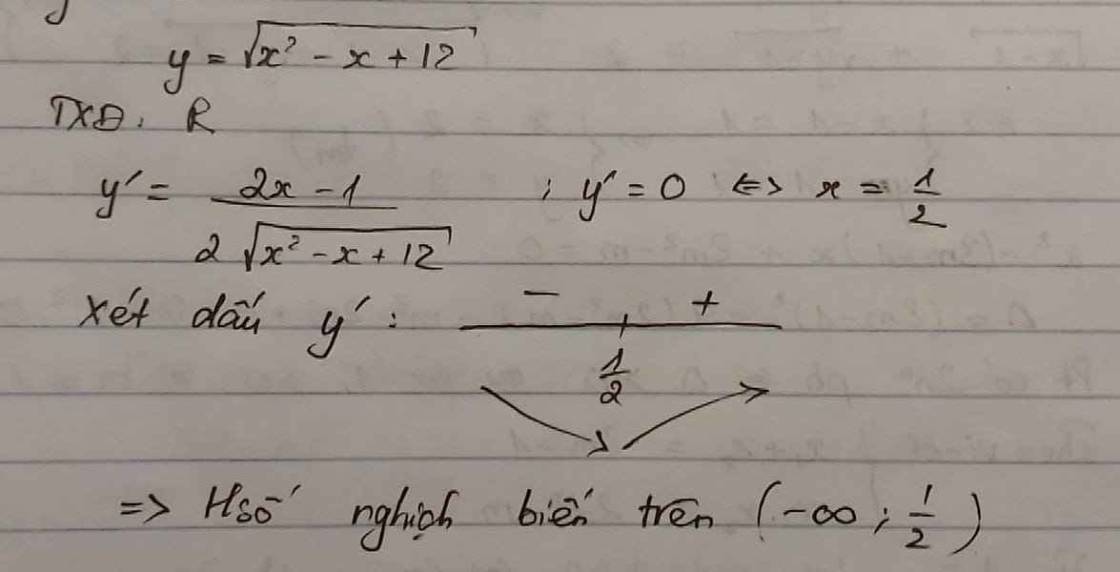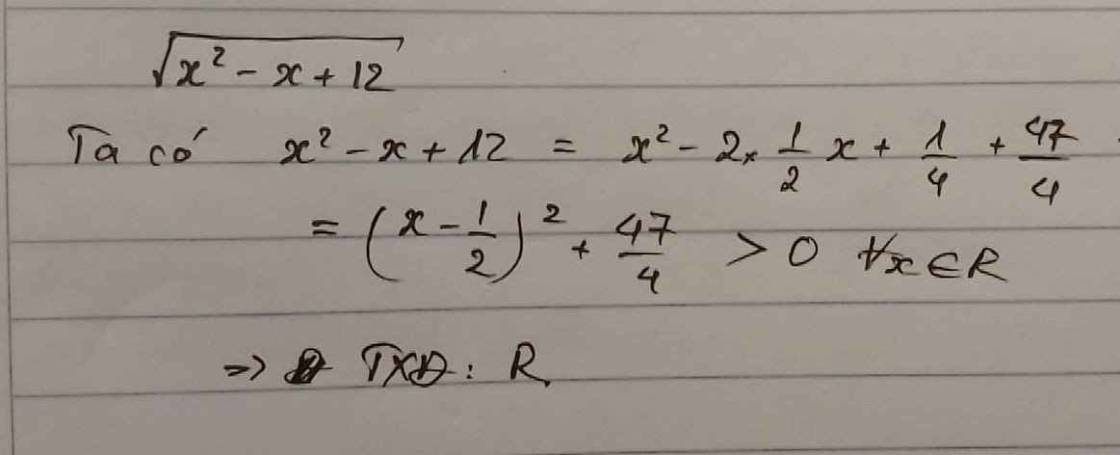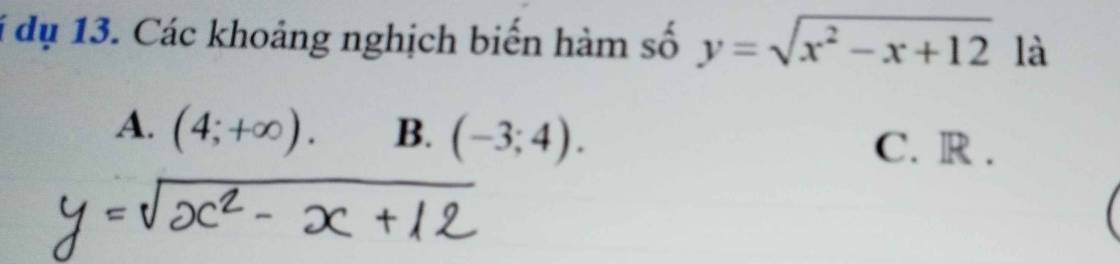c: Thay y=-x vào (P), ta được:

-x^2=-x

=>x^2=x

=>x(x-1)=0

=>x=0 hoặc x=1

Khi x=0 thì y=0

Khi x=1 thì y=-1

Vậy: Điểm cần tìm là M(1;-1) hoặc O(0;0)

b: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}-\dfrac{1}{4}x^2-\dfrac{1}{2}x=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x\left(\dfrac{1}{2}x+1\right)=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(0;0\right);\left(-2;-1\right)\right\}\)

c: Gọi M(2y;y)

Thay x=2y và y=y vào (P), ta được:

\(y=\dfrac{-1}{4}\cdot\left(2y\right)^2=\dfrac{-1}{4}\cdot4y^2=-y^2\)

=>y(y+1)=0

=>y=0 hoặc y=-1

=>x=0 hoặc x=-2

Câu 7:

b: Tọa độ của C là:

\(\left\{{}\begin{matrix}2x-3=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow C\left(4;5\right)\)

Tìm tọa độ trung điểm của AB là C (a;b) ạ 

Pt hoành độ giao điểm (P) và (d):

\(\dfrac{x^2}{2}=mx+\dfrac{1}{2}\Leftrightarrow x^2-2mx-1=0\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_M+x_N=2m\\x_Mx_N=-1\end{matrix}\right.\)

Gọi I là trung điểm MN \(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_M+x_N}{2}\\y_I=\dfrac{y_M+y_N}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_I=\dfrac{2m}{2}=m\\y_I=\dfrac{m.x_M+\dfrac{1}{2}+m.x_N+\dfrac{1}{2}}{2}=\dfrac{m\left(x_M+x_N\right)+1}{2}=m^2+\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow y_I=x_I^2+\dfrac{1}{2}\)

Hay tập hợp I là parabol có pt: \(y=x^2+\dfrac{1}{2}\)

a.

Pt hoành độ giao điểm (d) và (d'):

\(x+1=2x-2m-1\Leftrightarrow x=2m+2\)

\(\Rightarrow y=x+1=2m+3\)

2 đường thẳng cắt nhau tại 1 điểm nằm trong góc phần tư thứ II khi:

\(\left\{{}\begin{matrix}2m+2< 0\\2m+3>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -1\\m>-\dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow-\dfrac{3}{2}< m< -1\)

2 trục tung - hoành của hệ trục tọa độ cắt nhau chia mặt phẳng tọa độ làm 4 phần đánh dấu theo thứ tự ngược chiều kim đồng hồ, góc phần tư thứ I là phần tương ứng từ 12 giờ đến 3 giờ (ứng với x;y đều dương), góc phần tư thứ II từ 9 giờ đến 12h ( x âm y dương), góc III từ 6h đến 9h (x;y đều âm), góc IV từ 3h đến 6h (x dương  y âm)

b.

\(\Delta'=m^2-6m+9=\left(m-3\right)^2\ge0;\forall m\) nên pt luôn có 2 nghiệm

Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\\x_1x_2=6m-m^2\end{matrix}\right.\)

Do \(x_1\) là nghiệm nên \(x_1^2+6x_1+6m-m^2=0\Leftrightarrow2x_1^2+12x_1=2m^2-12m\)

Từ đó:

\(x_1^3-x_2^3+2x_1^2+12x_1+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left(\left(x_1+x_2\right)^2-x_1x_2\right)+2m^2-12m+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left(36+m^2-6m\right)+2\left(m^2-6m+36\right)=0\)

\(\Leftrightarrow\left(x_1-x_2+2\right)\left(m^2-6m+36\right)=0\)

Do \(m^2-6m+36=\left(m-3\right)^2+27>0;\forall m\)

\(\Rightarrow x_1-x_2+2=0\)

Kết hợp \(x_1+x_2=-6\) \(\Rightarrow\left\{{}\begin{matrix}x_1-x_2=-2\\x_1+x_2=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-4\\x_2=-2\end{matrix}\right.\)

Thế vào \(x_1x_2=6m-m^2\)

\(\Rightarrow6m-m^2=8\Rightarrow m^2-6m+8=0\Rightarrow\left[{}\begin{matrix}m=2\\m=4\end{matrix}\right.\)