Giúp mình bài này vs tối mình phải nộp rồi

Những câu hỏi liên quan
Mọi người ơi giúp mình 3 bài này với mình cần gấp gấp lắm ạ , tối nay mình phải nộp rồi ạ , cảm ơn mọi người❤️
Tỉ lệ \(x=\dfrac{y}{-5}\)
x -4 -1 2 3
y 20 5 -10 -15
Đúng 0
Bình luận (0)
Giúp mình vs tối nay mình phải nộp rồi!!Mình cám ơn trước nha!!!
Câu 1:
1: \(\overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\overrightarrow{OD}}{2}=\dfrac{\overrightarrow{BO}+\overrightarrow{OA}}{2}=\dfrac{\overrightarrow{BA}}{2}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
\(\overrightarrow{BD}=2\cdot\overrightarrow{BO}=-2\cdot\overrightarrow{OB}\)
nên y=-2
2: \(2\cdot\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{DO}+\overrightarrow{OC}=\overrightarrow{DC}=\overrightarrow{AB}\)
Vậy: Các vecto u thỏa mãn là vecto DC và vecto AB
Đúng 0
Bình luận (0)
Giúp mình vs tối nay mình phải nộp rồi😭😭😭, mình cám ơn trước nha!!!
Câu 1:
1: \(\overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\overrightarrow{OD}}{2}=\dfrac{\overrightarrow{BO}+\overrightarrow{OA}}{2}=\dfrac{\overrightarrow{BA}}{2}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
\(\overrightarrow{BD}=2\cdot\overrightarrow{BO}=-2\cdot\overrightarrow{OB}\)
nên y=-2
2: \(2\cdot\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{DO}+\overrightarrow{OC}=\overrightarrow{DC}=\overrightarrow{AB}\)
Vậy: Các vecto u thỏa mãn là vecto DC và vecto AB
Đúng 1
Bình luận (0)
Giúp mình bài này đi, tối nay mình phải nộp rùi.

Giúp mình bài 4 và vẽ hình luôn mn ơi. Tối mình phải nộp rồi😢
a/ Ta có:
- ABCD là hình bình hành => \(AD=BC;AD\text{ // }BC\)
- Xét △ADH và △BKC có:
+ \(AD=BC\left(cmt\right)\)
+ \(\hat{ADH}=\hat{CBK}\left(slt\right)\)
=> \(\text{△ADH = △CBK}\left(c.h-g.n\right)\)
Vậy: \(...
Đúng 0
Bình luận (0)
(Làm lại tại bị lỗi)
a/ - ABCD là hình bình hành => \(AD\text{//}BC;AD=BC\)
- Xét △ADH và △CBK có:
+ \(AD=BC\left(cmt\right)\)
+ \(\hat{ADH}=\hat{CBK}\left(slt\right)\)
=> \(\text{△ADH = △CBK }\left(c.h-g.n\right)\).
Vậy: \(DH=BK\left(đpcm\right)\)
==========
b/ \(AH\text{⊥}HK;CK\text{⊥}HK\)
=> \(AH\text{//}CK\)
Xét tứ giác AHCK có:
- \(AH=CK\left(\text{△ADH = △CBK }\right)\)
- \(AH\text{//}CK\)
Vậy: Tứ giác AHCK là hình bình hành (đpcm)
===========
c/ Hình bình hành AHCK có
- HK là đường chéo
- O là trung điểm của HK
=> O cũng là trung điểm của đường chéo AC (Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường)
Vậy: A, O, H thẳng hàng (đpcm)
Đúng 0
Bình luận (0)
Tìm GTNN của P = x^3+2021/x Giúp mình với m.b ui tối này mình phải nộp cho cô ròi mà vẫn không bt lm câu này m.n giúp mình vs ạ
- Bài này phải có điều kiện \(x>0\) thì mới làm được nhé bạn.
Đúng 1
Bình luận (2)
\(P=\dfrac{x^3+2021}{x}=x^2+\dfrac{2021}{x}=x^2+\dfrac{2021}{2x}+\dfrac{2021}{2x}\)
Áp dụng bất đẳng thức Cauchy cho 3 số dương ta có:
\(x^2+\dfrac{2021}{2x}+\dfrac{2021}{2x}\ge3\sqrt[3]{x^2.\dfrac{2021}{2x}.\dfrac{2021}{2x}}=3\sqrt[3]{\dfrac{2021^2}{4}}\)
Dấu "=" xảy ra khi \(x^2=\dfrac{2021}{2x}\Leftrightarrow x=\sqrt[3]{\dfrac{2021}{2}}\)
Vậy \(MinP=3\sqrt[3]{\dfrac{2021^2}{4}}\)
Đúng 0
Bình luận (0)
Ai giúp mình bài này với. 15p nữa mình phải nộp rồi :(
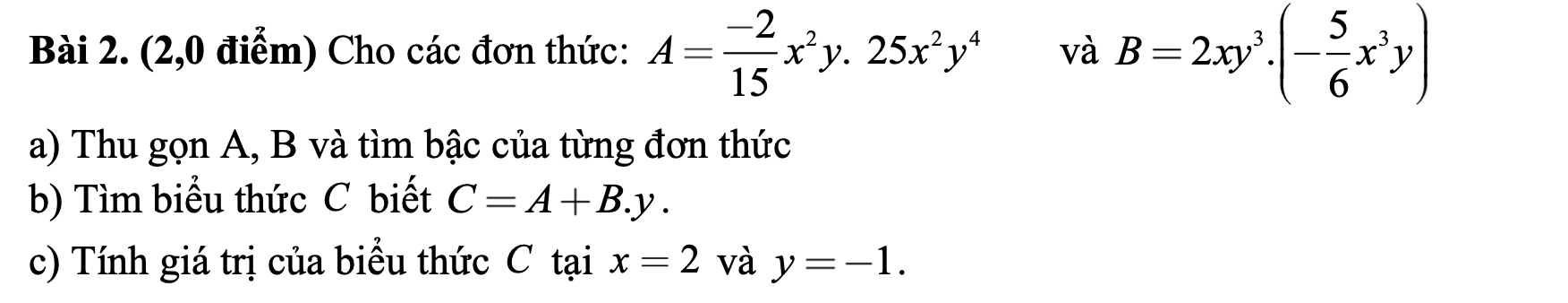
a: A=-2/15*25*x^2y*x^2y^4=-10/3*x^4y^5
B=2*(-5/6)*xy^3*x^3y=-5/3*x^4y^4
b: C=A+B*y
=-10/3*x^4y^5-5/3*x^4y^5
=-5x^4y^5
c: Khi x=2 và y=-1 thì C=-5*2^4*(-1)^5=5*16=80
Đúng 0
Bình luận (0)
Các bạn làm giúp mình mấy bài này mai mình phải nộp rồi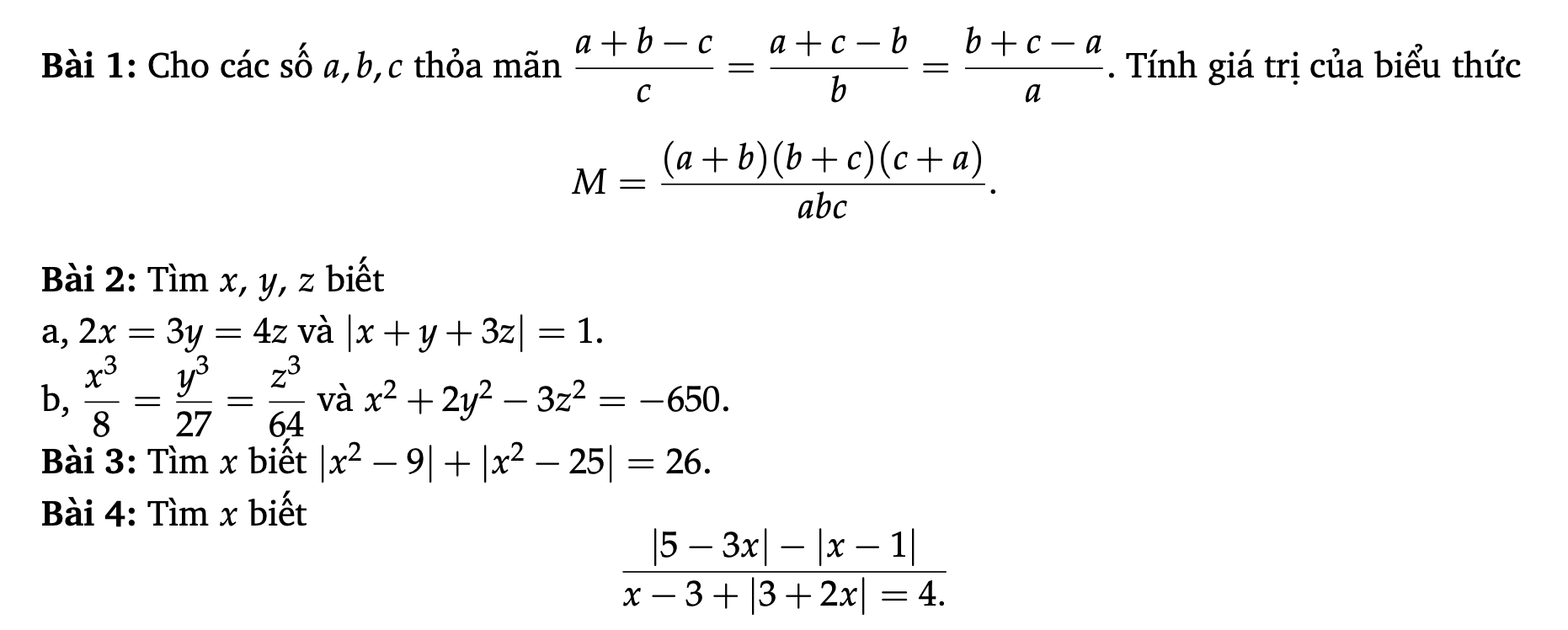
1, \(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)
=> \(\dfrac{a+b}{c}-1=\dfrac{a+c}{b}-1=\dfrac{b+c}{a}-1\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}=\dfrac{a+b+a+c+b+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
=> \(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{a+b}{c}\times\dfrac{a+c}{b}\times\dfrac{b+c}{a}=2.2.2=8\)
=> \(M=8\)
Đúng 1
Bình luận (3)
Các bạn làm giúp mình mấy bài này mai mình phải nộp rồi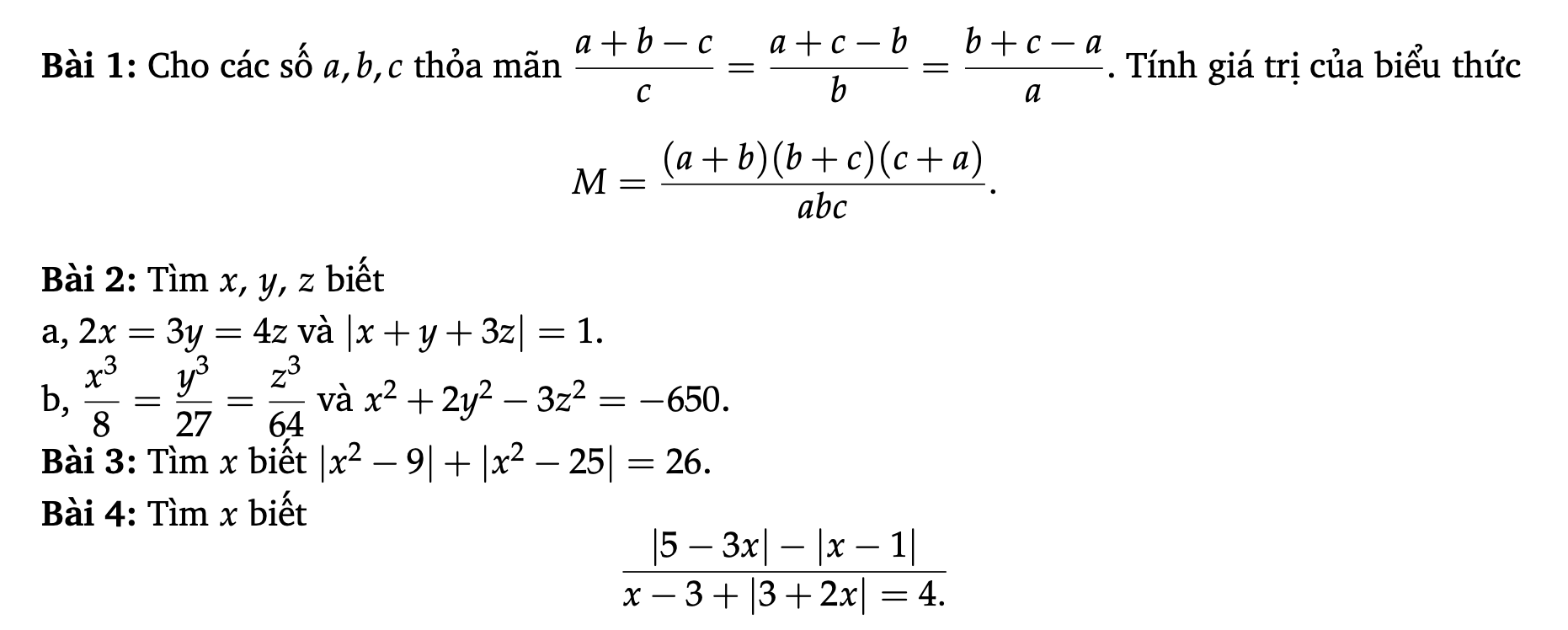
Bài 1:
Nếu $a+b+c=0$ thì đkđb thỏa mãn
$M=\frac{(-c)(-a)(-b)}{abc}=\frac{-(abc)}{abc}=-1$
Nếu $a+b+c\neq 0$. Áp dụng TCDTSBN:
$\frac{a+b-c}{c}=\frac{a+c-b}{b}=\frac{b+c-a}{a}=\frac{a+b-c+a+c-b+b+c-a}{c+b+a}=\frac{a+b+c}{a+b+c}=1$
$\Rightarrow a+b-c=c; a+c-b=b; b+c-a=a$
$\Leftrightarrow a+b=2c; a+c=2b; b+c=2a$
$\Rightarrow a=b=c$
$M=\frac{(a+a)(a+a)(a+a)}{aaa}=\frac{8a^3}{a^3}=8$
Đúng 1
Bình luận (0)
Bài 2a
Đặt $2x=3y=4z=t$
$\Rightarrow x=\frac{t}{2}; y=\frac{t}{3}; z=\frac{t}{4}$
Khi đó:
$|x+y+3z|=1$
$\Leftrightarrow |\frac{t}{2}+\frac{t}{3}+\frac{3t}{4}|=1$
$\Leftrightarrow |\frac{19}{12}t|=1$
$\Rightarrow t=\pm \frac{12}{19}$
Nếu $t=\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{6}{19}; y=\frac{4}{19}; z=\frac{3}{19}$
Nếu $t=-\frac{12}{19}$ thì:
$x=\frac{t}{2}=\frac{-6}{19}; y=\frac{-4}{19}; z=\frac{-3}{19}$
Đúng 1
Bình luận (0)
Bài 2b:
$\frac{x^3}{8}=\frac{y^3}{27}=\frac{z^3}{64}$
$\Leftrightarrow (\frac{x}{2})^3=(\frac{y}{3})^3=(\frac{z}{4})^3$
$\Leftrightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+2y^2-3z^2=-650$
$\Leftrightarrow (2t)^2+2.(3t)^2-3(4t)^2=-650$
$\Leftrightarrow -26t^2=-650$
$\Leftrightarrow t=\pm 5$
Nếu $t=5$ thì:
$x=2t=10; y=3t=15; z=4t=20$
Nếu $t=-5$ thì:
$x=2t=-10; y=3t=-15; z=4t=-20$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
















