1, \(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}\)
=> \(\dfrac{a+b}{c}-1=\dfrac{a+c}{b}-1=\dfrac{b+c}{a}-1\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}\)
=> \(\dfrac{a+b}{c}=\dfrac{a+c}{b}=\dfrac{b+c}{a}=\dfrac{a+b+a+c+b+c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
=> \(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{a+b}{c}\times\dfrac{a+c}{b}\times\dfrac{b+c}{a}=2.2.2=8\)
=> \(M=8\)


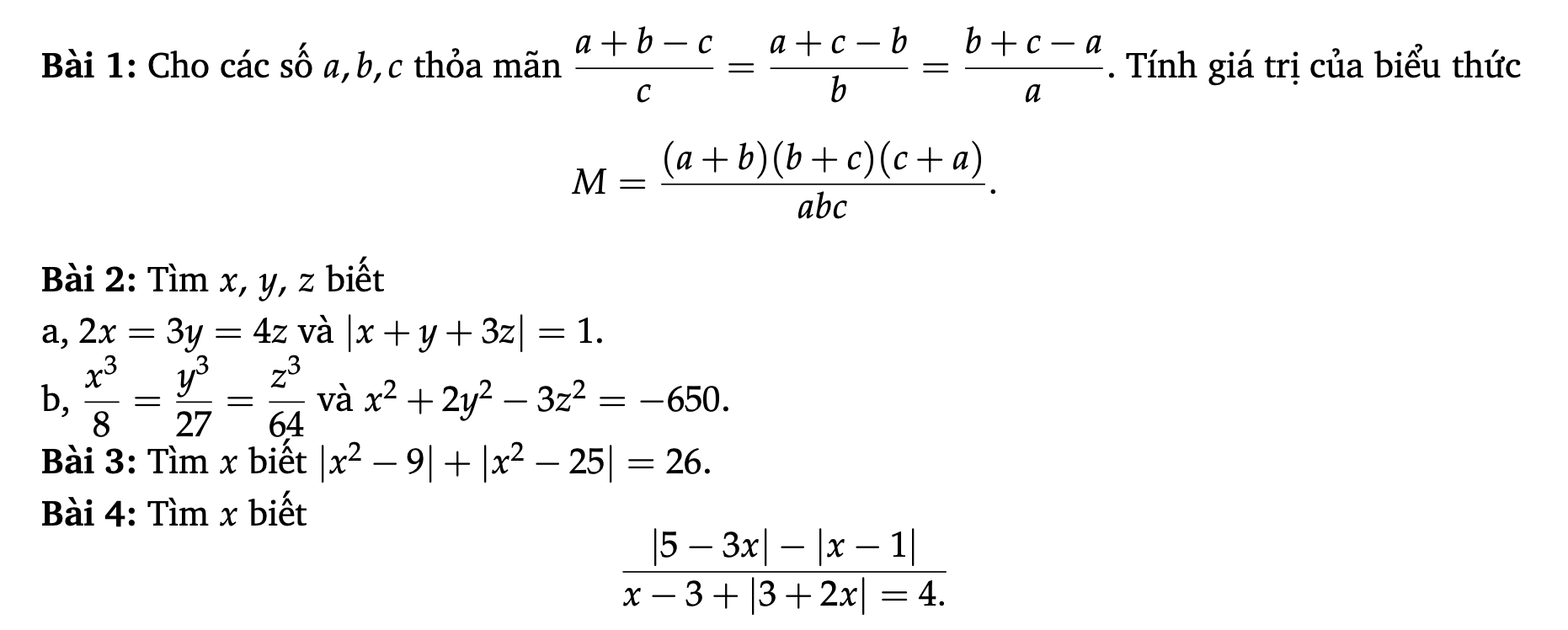


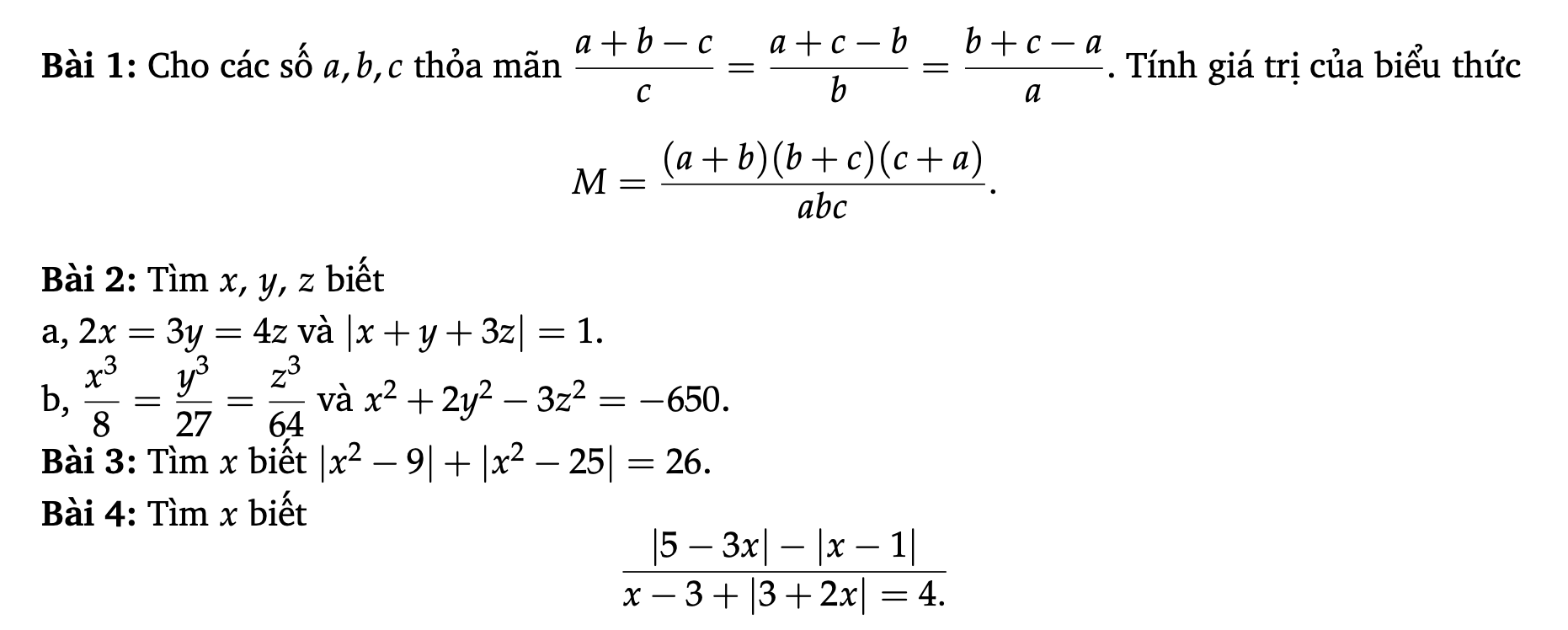
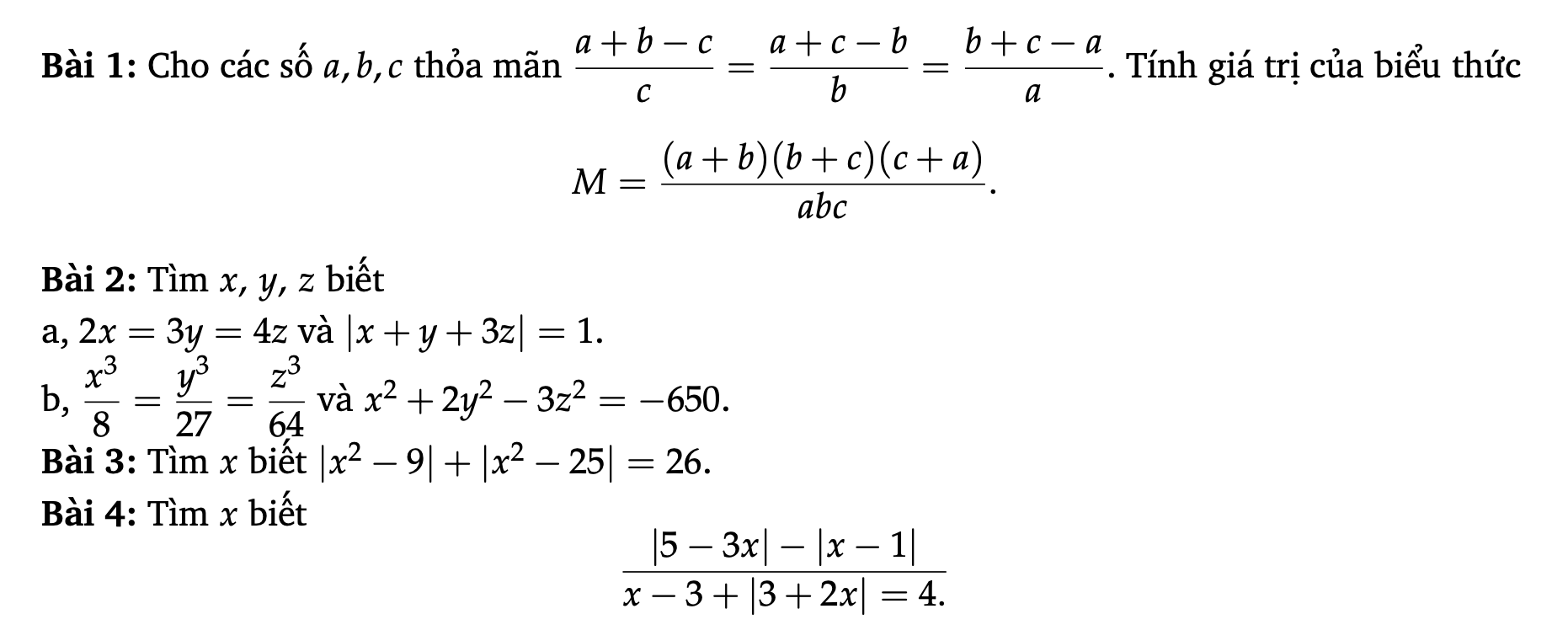
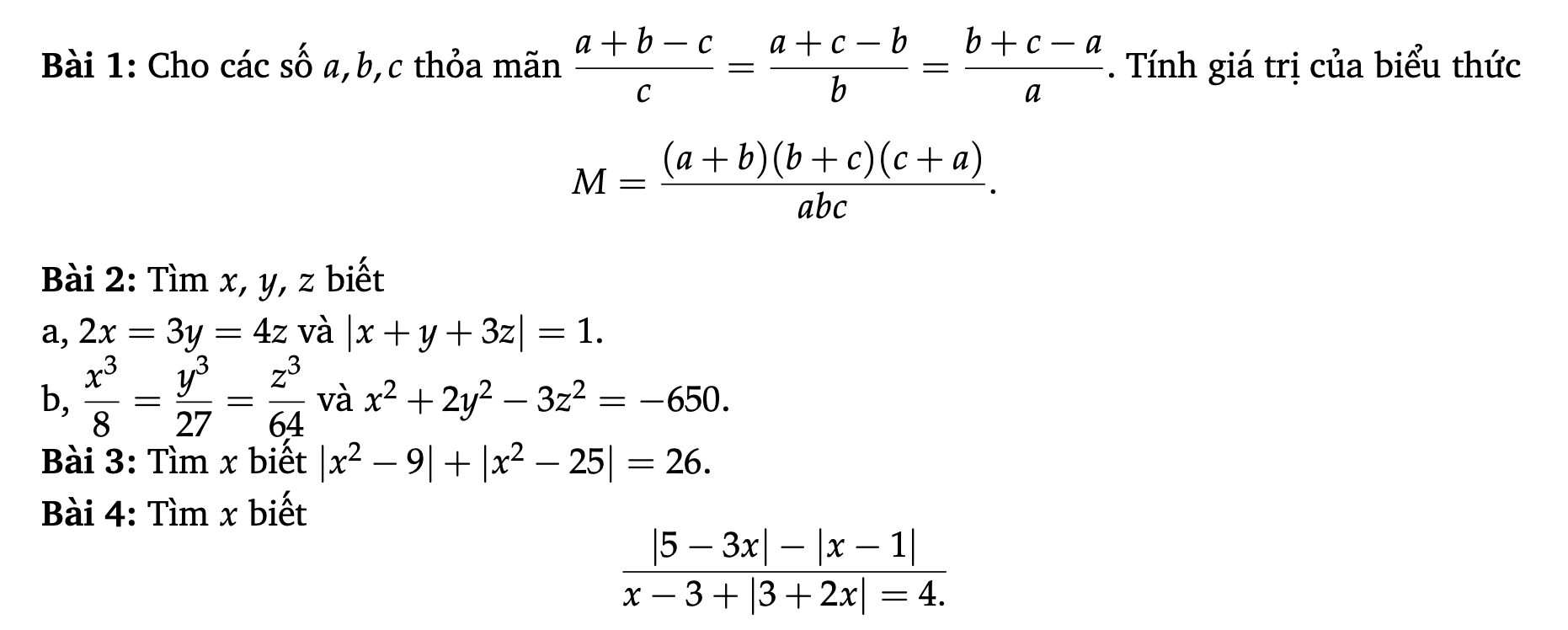


 Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔
Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔

