1. TH1:a+b+c≠0
Áp dụng t/c dtsbn ta có:
\(\dfrac{a+b-c}{c}=\dfrac{a+c-b}{b}=\dfrac{b+c-a}{a}=\dfrac{a+b-c+a+c-b+b+c-a}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\dfrac{a+b-c}{c}=1\Rightarrow a+b-c=c\Rightarrow a+b=2c\\ \dfrac{a+c-b}{b}=1\Rightarrow a+c-b=b\Rightarrow a+c=2b\\ \dfrac{b+c-a}{a}=1\Rightarrow b+c-a=a\Rightarrow b+c=2a\)
\(=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\\ =\dfrac{2c.2a.2b}{abc}\\ =\dfrac{8abc}{abc}\\ =8\)
TH2:a+b+c=0
\(\Rightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\c+a=-b\end{matrix}\right.\)
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{-c.-a.-b}{abc}=\dfrac{-abc}{abc}=-1\)
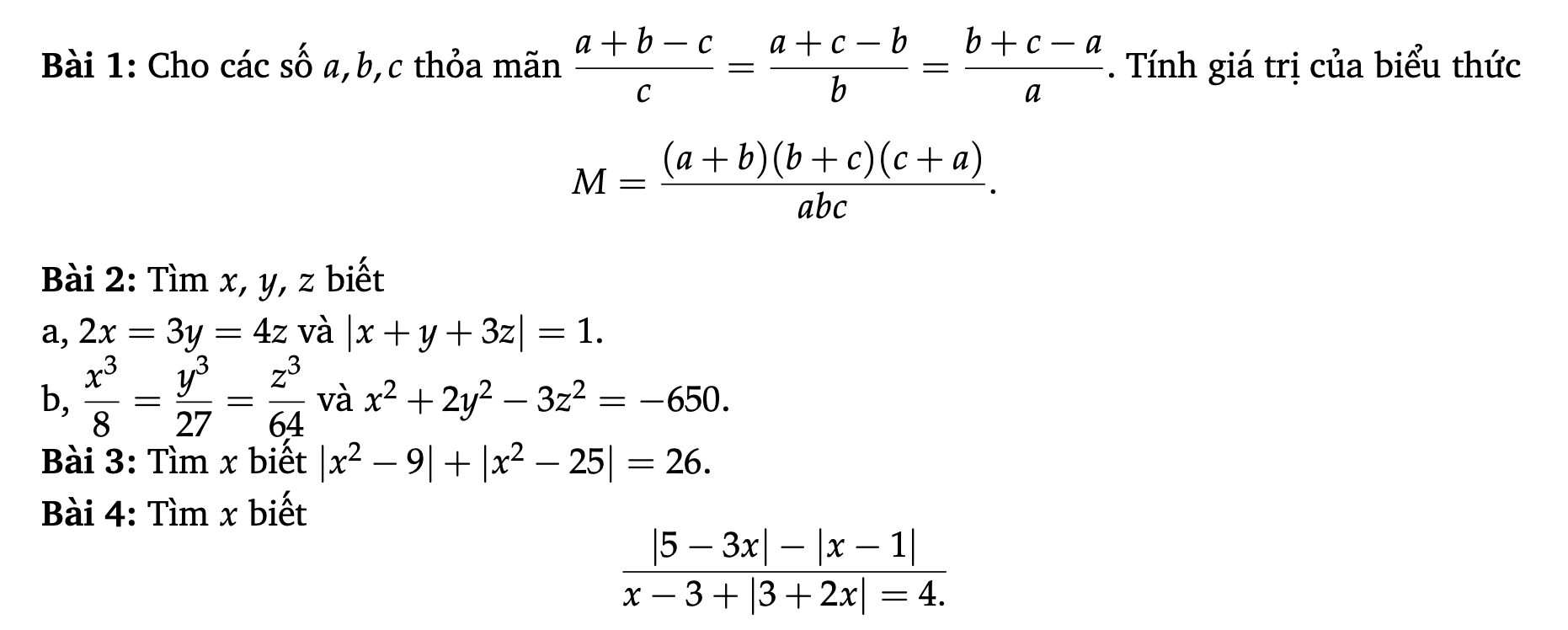
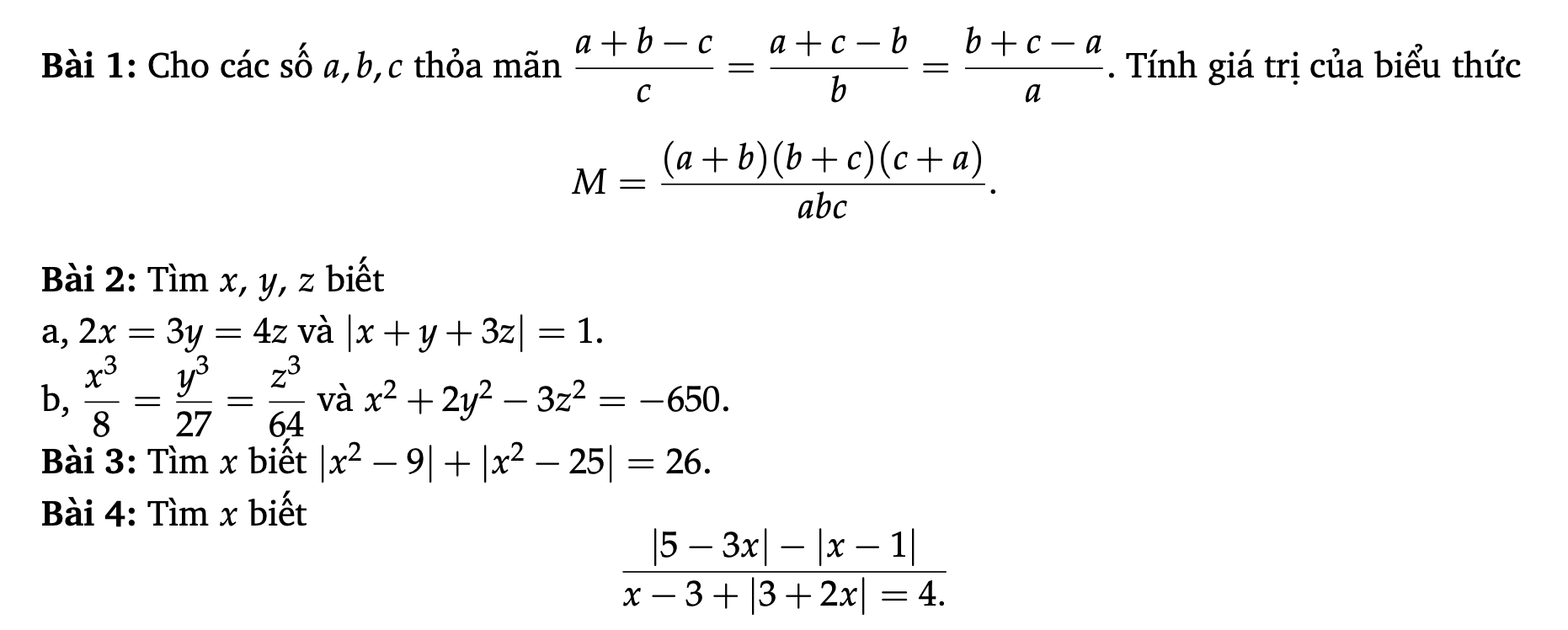
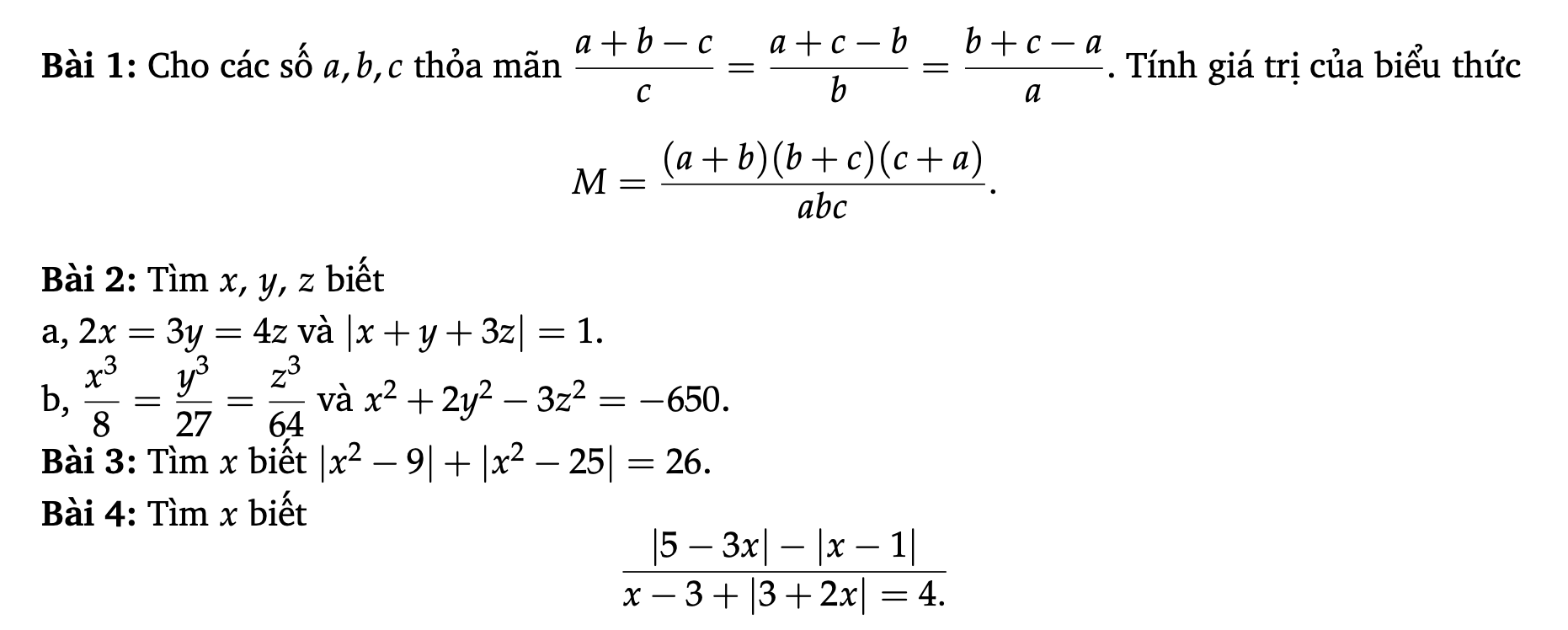
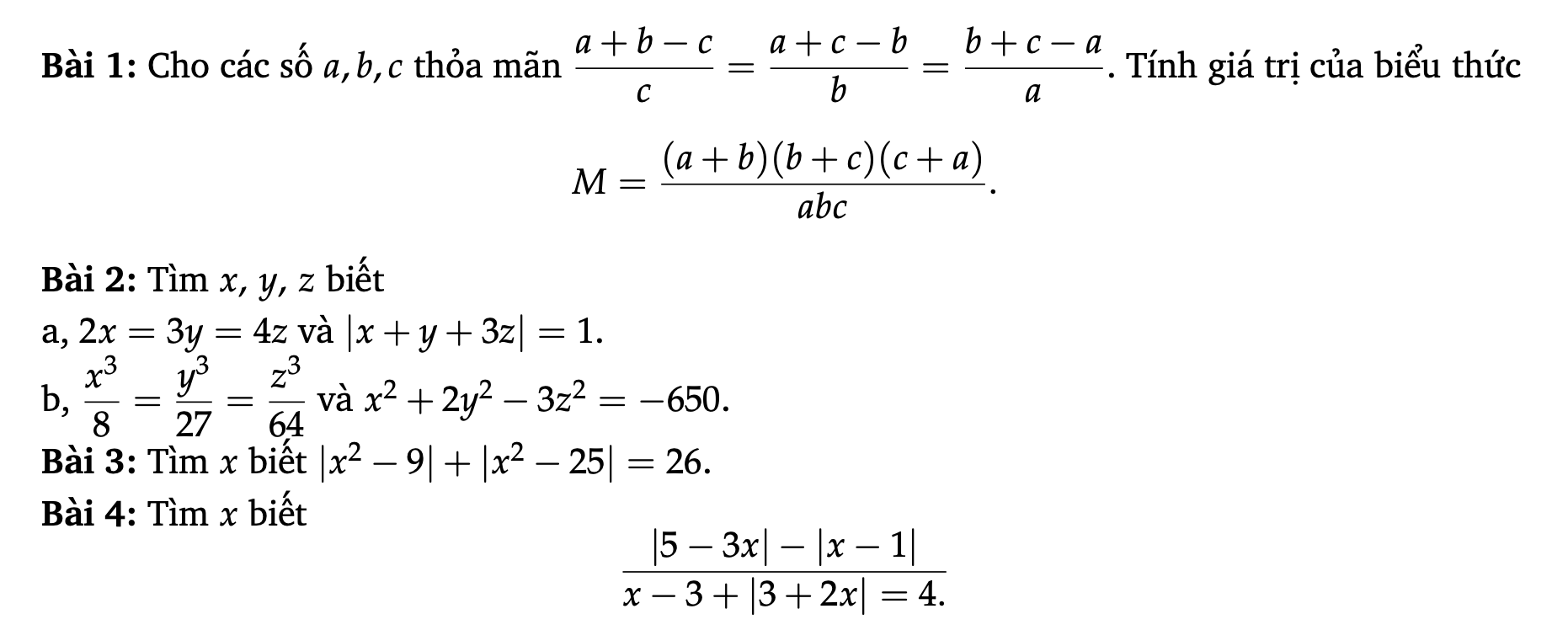
Các bạn giúp mình làm mấy bài này ngày mai mình phải nộp rồi 😔
