Cho tam giác ABC có BD,CE là các phân giác . CMR : Nếu BD=CE thì tam giác ABC cân tại A

Những câu hỏi liên quan
Cho tam giác abc có bd và ce là phân giác cắt nhau tại i . cmr: nếu bi*ci=1/2 bd*ce thì tam giác abc vuông
CHO TAM GIÁC ABC CÂN TẠI A. VẼ CÁC ĐƯỜNG PHÂN GIÁC BD, CE
a. CMR: BD=CE b. BD CẮT CE TẠI I. CMR: TAM GIÁC BIC CÂN VÀ TAM GIÁC BIE= TAM GIÁC CID
c. CMR:AI VUÔNG GÓC VS ED VÀ ED // BC
a/ ta có \(\hept{\begin{cases}\widehat{ACE}=\widehat{BCE}=\widehat{\frac{ACB}{2}}\\\widehat{ABD}=\widehat{CBD}=\widehat{\frac{ABC}{2}}\end{cases}}\)( tia phân giác )
mà \(\widehat{ACB}=\widehat{ABC}\)( tam giác cân)
nên ACE=BCE=ABD=CBD
xét tam giác ABD và tam giác ACE có
ABD=ACE(cmt) ; góc A chung ; AB=AC(tam giác cân)
=> tam giác ABD=tam giác ACE (G-C-G) => BD=CE
b/ ta có BCE=CBD (cmt) => tam giác BIC cân tại I
xét tam giácBIE và tam giác CID có
BI=IC(tam giác BIC cân) ; BIE=ICD(ABD=ACE) ; BIE=CID(2 góc đối đỉnh)
=> tam giác BIE= tam giác CID (G-C-G)
c/ ta có BD, CE là tia p/g cắt nhau tại I => I là gđ của 3 đg phân giác của tam giác ABC
=> AI là tia phân giác của BAC
ta có AB=AE+BE ; AC=AD+DC
mà BE=CD ( tam giác BIE= tam giác CID) ; AB=AC (tam giác ABC cân)
nên AE=AD => tam giác AED cân
mặt khác AI là tia phân giác => AI là đường cao => AI vuông góc vs ED
ta có \(\hept{\begin{cases}\widehat{AED}=\frac{180^0-\widehat{A}}{2}\\\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\end{cases}}\)(tam giác cân)
=> AED=ABC
mà 2 góc nằm ở vị trí đồng vị => ED//BC
Đúng 0
Bình luận (0)
A) Ta có \(\Delta\)ABC cân tại A =>góc ABC= góc ACB => \(\frac{1}{2}\)góc ABC =\(\frac{1}{2}\)góc ACB => góc DBC = góc ECB = góc DBE = góc DCE
Xét \(\Delta\)ECB và \(\Delta\)DBC có
-góc DBC = góc ECB
- BC chung
-góc EBC = góc DCB
=> \(\Delta\)ECB = \(\Delta\)DBC ( g.c.g )
=> CE =BD
B, Ta có góc IBC = góc ICB ( góc DBC =góc ECB chứng minh trên )
=> \(\Delta\)IBC cân tại I => BI = CI
Xét \(\Delta\)BIE và \(\Delta\)CID có
- góc BIE = góc CID ( 2 góc đối đỉnh )
- IB =CI ( chứng minh trên )
- góc IBE =ICD ( chứng minh trên ý a )
=> \(\Delta\)BIE =\(\Delta\)CID (g.c.g)
C, Ta có AB =AC ( \(\Delta\)ABC cân tại A )
Mà BE =CD ( \(\Delta\) EBD =\(\Delta\)DCE )
=> AE =AD (1)
Lại có BD =CE ( chứng minh trên ý a )
Mà BI =CI ( chứng minh trên )
=> EI =ID (2)
Từ (1) và (2) => AI là đường trung trực của ED
=> AI \(⊥\)ED
Ta có \(\Delta\)EAD cân tại A có Ai là đường phân giác => góc EAI = góc DAI
Lại có \(\Delta\)ABC cân tại A có AI là tia phân giác đồng thời là đường cao => AI \(⊥\)BC
\(\hept{\begin{cases}AI⊥DE\\AI⊥BC\end{cases}}\)
=> ED sog sog BC
Chúc bạn học giỏi
Kết bạn với mình nha
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có các đường phân giác BD, CE . Chứng minh BD=CE.
Có `Delta ABC` cân tại `A=>AB=AC;hat(ABC)=hat(ACB)`
Có `hat(ABC)=hat(ACB)(cmt)`
mà `BD` là p/g `hat(ABC)`
`CE` là p/g `hat(ACB)`
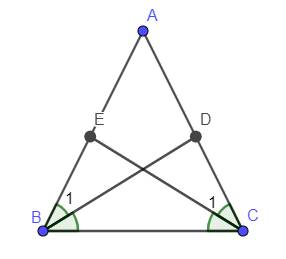
nên `hat(B_1)=hat(C_1)`
Xét `Delta ABD` và `Delta ACE` có :
`{:(hat(B_1)=hat(C_1)(cmt)),(AB=AC(cmt)),(hat(A)-chung):}}`
`=>Delta ABD=Delta ACE(g.c.g)`
`=>BD=CE` ( 2 cạnh t/ứng )(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có các đường phân giác BD, CE . Chứng minh BD=CE.
BD là đường phân giác của góc B nên ta có :
\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CE là đường phân giác của góc C nên ta có :
\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Từ ( 1 ) , ( 2 ) = > \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ADB và tam giác AEC ta có :
Góc A chung
AB = AC ( gt )
\(\widehat{ABD}=\widehat{ACE}\) ( cmt )
= > \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
= > BD = CE ( 2 cạnh tương ứng )
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, A<90, kẻ BD vuông góc với AC tại D kẻ Ce vuông góc với AB tại E. Gọi K là giao điểm của BD và CE .CMR: A)tam giác BCE= tam giác CBD. B) tam giác BEK=tam giác CDK. C) AK là tia phân giác của BAC
Giúp mik vs các bẹn
a) Xét tam giác BCE vuông tại E và tam giác CBD vuông tại D:
BC chung.
Góc B = Góc C (Tam giác ABC cân tại A).
=> Tam giác BCE = Tam giác CBD (cạnh huyền - góc nhọn).
b) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E:
Góc A chung.
AB = AC (Tam giác ABC cân tại A).
=> Tam giác ABD = Tam giác ACE (cạnh huyền - góc nhọn).
=> Góc ABD = Góc ACE (2 góc tương ứng).
Xét tam giác BEK và tam giác CDK:
Góc EBK = Góc DCK (Góc ABD = Góc ACE).
BE = CD (Tam giác BCE = Tam giác CBD).
Góc BEK = Góc CDK (= 90o).
=> Tam giác BEK = Tam giác CDK (g - c - g).
c) Xét tam giác ABC:
BD là đường cao (BD vuông góc với AC).
CE là đường cao (CE vuông góc với AB).
BD cắt CE tại K (gt).
=> K là trực tâm.
=> AK là đường cao.
Xét tam giác ABC cân tại A: AK là đường cao (cmt).
=> AK là đường phân giác góc BAC (Tính chất các đường trong tam giác cân).
Đúng 1
Bình luận (0)
Cho tam giác ABC, BD và CE là 2 đường trung tuyến. Chứng minh nếu BD= CE thì tam giác ABC cân
Gọi giao của BD và CE là G
=>G là trọngtâm của ΔABC
=>BG=2/3BD; CG=2/3CE
mà BD=CE
nên GB=GC
Xét ΔEBC và ΔDCB có
BC chung
góc ECB=góc DBC
EC=DB
=>ΔEBC=ΔDCB
=>góc EBC=góc DCB
=>ΔABC cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Từ B và C lần lượt BD và CE vuông góc với các đường thẳng AC và AB tại D và E .Gọi AH là đường cao của tam giác ABC.
a,CM: tam giác ABD=tam giác ACE
b,Nếu góc ABD=40 độ thì góc BAC = bao nhiêu độ
c,CMR:3 đường AH,BD,CE đồng quy
Cho tam giác ABC có các đường phân giác BD,CE bằng nhau .Chứng minh rằng :tam giác ABC cân tại A.
ko trả lời cũng k bạn rảnh quá ha
Đúng 0
Bình luận (0)
cho tam giác ABC có BD và CE là 2 đường cao hạ từ B,C và BD=CE. H là giao điểm của BD và CE
a) Chứng minh tam giác ABC cân tại A
b) AH là phân giác góc BAC





















