Làm dùm e bài này với ạ

Những câu hỏi liên quan
Hoàn thành câu 1 dùm e với ạ.
CÁC CHUYÊN GIA HÓA HỌC GIÚP E BÀI NÀY VỚI Ạ. 
MN LÀM dùm e đề này với ạ. 

Làm dùm e bài 7 với ạ
ĐKXĐ: \(x\ge4\)
\(\sqrt{x+11}\ge\sqrt{x-4}+\sqrt{2x-1}\)
\(\Leftrightarrow x+11\ge3x-5+2\sqrt{\left(x-4\right)\left(2x-1\right)}\)
\(\Leftrightarrow8-x\ge\sqrt{2x^2-9x+4}\)
\(\Leftrightarrow\left\{{}\begin{matrix}8-x\ge0\\\left(8-x\right)^2\ge2x^2-9x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\x^2+7x-60\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le8\\-12\le x\le5\end{matrix}\right.\) \(\Rightarrow-12\le x\le5\)
Kết hợp ĐKXD ta được nghiệm của BPT là: \(4\le x\le5\)
Đúng 2
Bình luận (1)
Làm dùm e bài 27 với ạ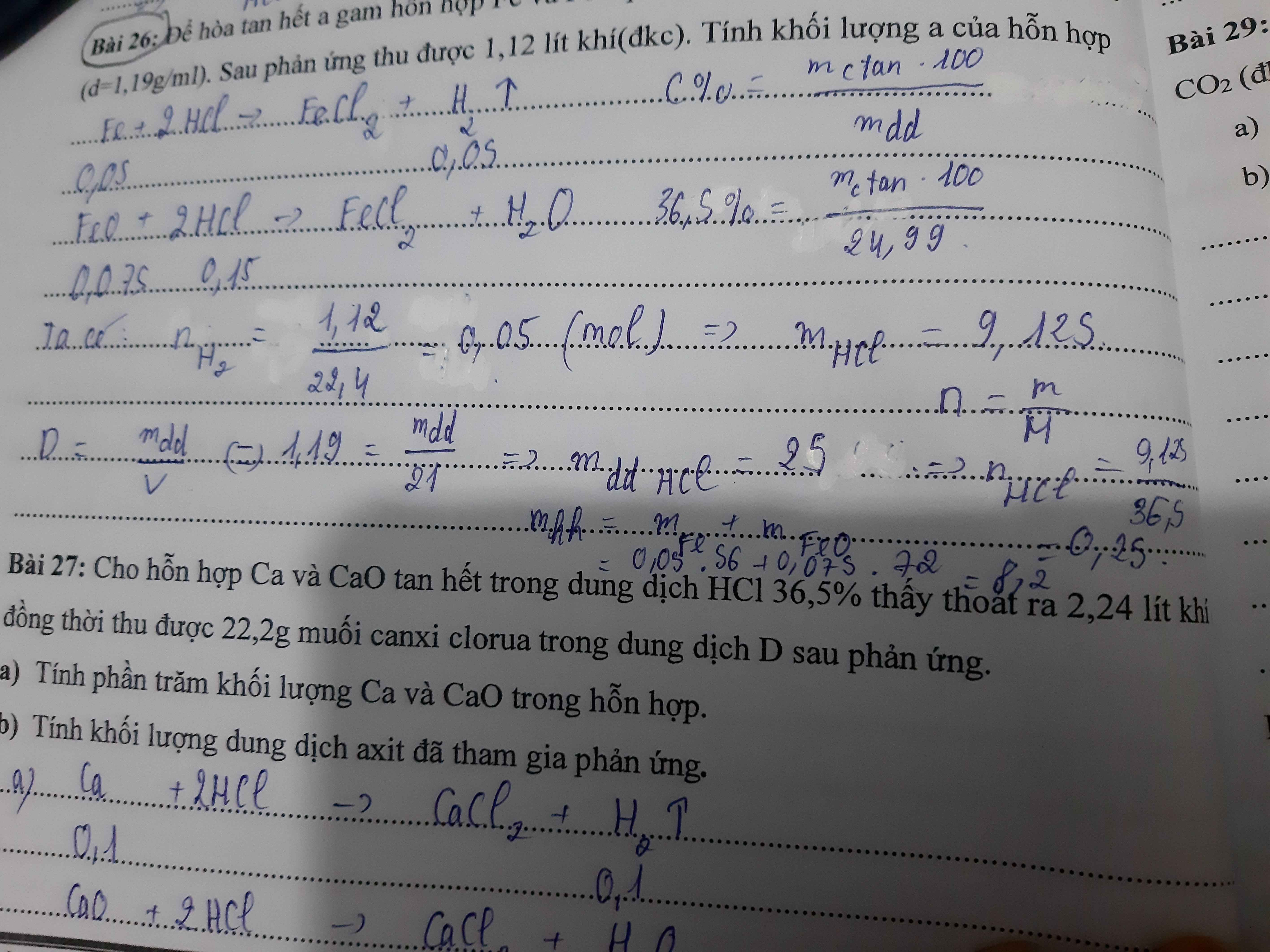
\(a,Ca+2HCl\rightarrow CaCl_2+H_2\left(1\right)\\ CaO+2HCl\rightarrow CaCl_2+H_2O\left(2\right)\\ Đặt:n_{Ca}=a\left(mol\right);n_{CaO}=b\left(mol\right)\\ \Rightarrow\left\{{}\begin{matrix}111a+111b=22,2\\22,4a=2,24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\\ \Rightarrow\%m_{CaO}=\dfrac{0,1.56}{0,1.56+0,1.40}.100\approx52,83\%\\ \Rightarrow\%m_{Ca}=47,17\%\\ b,n_{HCl}=2.\left(a+b\right)=0,4\left(mol\right)\\ \Rightarrow m_{ddHCl}=\dfrac{0,4.36,5.100}{36,5}=40\left(g\right)\)
Đúng 3
Bình luận (0)
Mn làm dùm 2 bài này với ạ.
Ghi rõ lời giải tóm tắt dùm e với ạ.
Câu 2.
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot m\cdot6^2+m\cdot10\cdot0=18m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\Rightarrow h_{max}=\dfrac{18}{10}=1,8m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\Rightarrow z=\dfrac{18}{2g}=\dfrac{18}{2\cdot10}=0,9m\)
c)Cơ năng tại nơi \(W_đ=2W_t\):
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{18}{3\cdot10}=0,6m\)
Đúng 2
Bình luận (0)
Làm dùm e bài này với ạ. Có tóm tắt và lời giải đầy đủ dùm e với ạ 
Bài 2.
Tóm tắt:
\(v=6\)m/s, \(g=10\)m/s2
a)\(h_{max}=?\)
b)\(W_t=W_đ\Rightarrow z=?\)
c)\(W_đ=2W_t\Rightarrow z'=?\)
Giải chi tiết:
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot6^2=18m\left(J\right)\)
a)Tại nơi có độ cao \(h_{max}\): \(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{18}{g}=\dfrac{18}{10}=1,8m\)
b)Tại nơi thế năng bằng động năng thì cơ năng là
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\)
\(\Rightarrow z=\dfrac{18}{2g}=\dfrac{9}{10}=0,9m\)
c)Tại nơi động năng bằng hai lần thế năng:
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{6}{10}=0,6m\)
Đúng 3
Bình luận (0)
Bài 3.
a)Cơ năng ban đầu: \(W=W_đ+W_t\)
\(\Rightarrow W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}m\cdot0^2+m\cdot10\cdot20=200m\left(J\right)\)
Cơ năng tại nơi vận tốc vật khi cham đất:
\(W'=\dfrac{1}{2}mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow200m=\dfrac{1}{2}mv'^2\)
\(\Rightarrow v'=20\)m/s
Cách khác nè:Áp dụng công thức( chỉ sử dụng khi tính vận tôc vật chạm đất)
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot20}=20\)m/s
b)Tại nơi có thế năng bằng động năng thì cơ năng là:
\(W_1=W_t+W_đ=2W_t=2mgh\)
Bảo toàn cơ năng: \(W_1=W\)
\(\Rightarrow2mgh=200m\)
\(\Rightarrow h=10m\)
c)Cơ năng tại nơi thế năng gấp 3 động năng:
\(W_2=W_đ+W_t=W_đ+3W_đ=4W_đ=4\cdot\dfrac{1}{2}mv'^2=2mv'^2\)
Bảo toàn cơ năng: \(W_2=W\)
\(\Rightarrow200m=2mv'^2\)
\(\Rightarrow v'=10\)m/s
Đúng 3
Bình luận (0)
Mn làm dùm e bài này với ạ.
Viết đầy đủ lời giải tóm tắt (vẽ hình) dùm e với ạ. 
Câu 7,8,10 MN làm giúp e với ạ. Ghi rõ cách làm dùm e với ạ. 
7.
ĐKXĐ: \(3\le x\le7\)
\(x-5+\sqrt{7-x}-\sqrt{x-3}=0\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x-3}=a\ge0\\\sqrt{7-x}=b\ge0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=2\left(x-5\right)\)
Pt trở thành:
\(\dfrac{a^2-b^2}{2}+b-a=0\)
\(\Leftrightarrow\left(a-b\right)\left(a+b-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a+b=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=\sqrt{7-x}\\\sqrt{x-3}+\sqrt{7-x}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=7-x\\4+2\sqrt{\left(x-3\right)\left(7-x\right)}=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=5\\x=7\end{matrix}\right.\)
Đúng 1
Bình luận (0)
8.
ĐKXĐ: \(-2\le x\le2\)
Đặt \(\sqrt{x+2}+\sqrt{2-x}=t\Rightarrow2\le t\le2\sqrt{2}\)
\(t^2=4+2\sqrt{4-x^2}\Rightarrow2\sqrt{-x^2+4}=t^2-4\)
Pt trở thành:
\(t+t^2-4+2m+3=0\)
\(\Leftrightarrow t^2+t+1=-2m\)
Xét hàm \(f\left(t\right)=t^2+t+1\) trên \(\left[2;2\sqrt{2}\right]\)
\(a=1>0;-\dfrac{b}{2a}=-\dfrac{1}{2}< 2\Rightarrow f\left(t\right)\) đồng biến trên đoạn đã cho
\(\Rightarrow f\left(2\right)\le f\left(t\right)\le f\left(2\sqrt{2}\right)\Rightarrow7\le f\left(t\right)\le9+2\sqrt{2}\)
\(\Rightarrow7\le-2m\le9+2\sqrt{2}\Rightarrow-\dfrac{9+2\sqrt{2}}{2}\le m\le-\dfrac{7}{2}\)
\(\Rightarrow m=\left\{-5;-4\right\}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
MN LÀM dùm e đề này với ạ.









