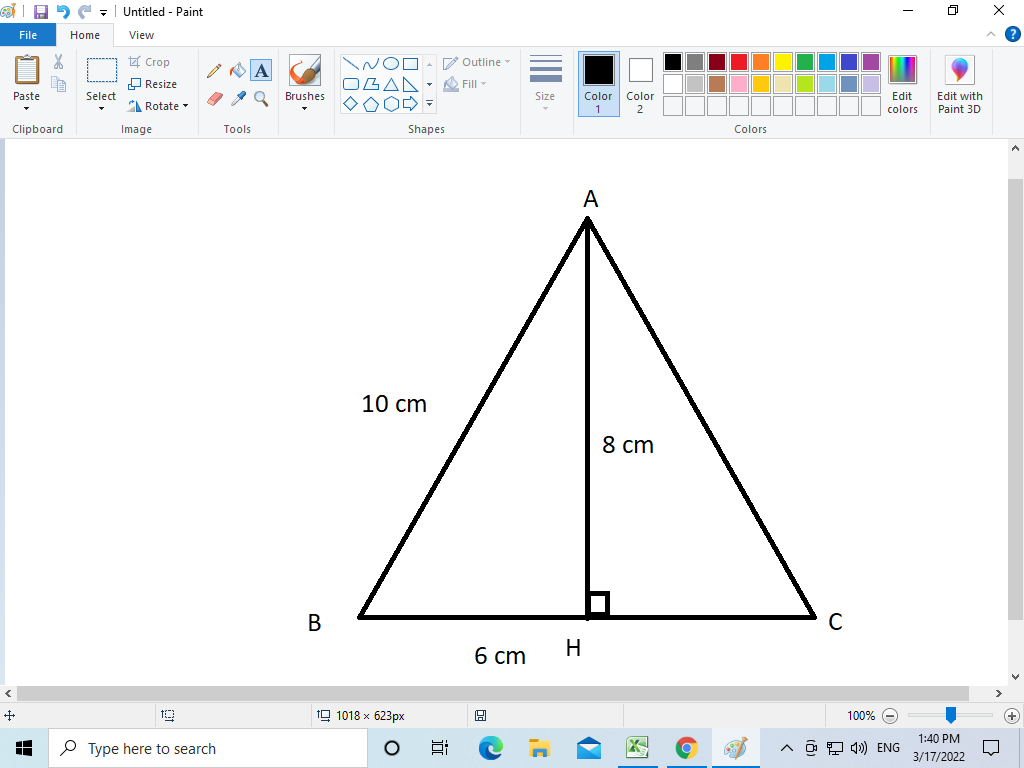
Cho tam giác ABC cân tại A vẽ AH vuông góc với BC tại H.Biết AB=10cm;BH==6cm
a)tính AH
b)tam giác ABD = tam giác ACH
c) trên BA lấy D,CA lấy E sao cho BD = CE . Chứng minh tam giác HDE cân
d) Chứng minh AH là trung trực của DE
Cho tam giác ABC cân tại A vẽ AH vuông góc với BC tại H.Biết AB=10cm;BH==6cm
a)tính AH
b)tam giác ABD = tam giác ACH
c) trên BA lấy D,CA lấy E sao cho BD = CE . Chứng minh tam giác HDE cân
d) Chứng minh AH là trung trực của DE
a, Xét tam giác HBA vuông tại H có:
AB2=AH2+BH2(định lí py ta go)
hay 100=AH2+36
=> AH2=64
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
d) Vì AB = AC; BD = CE
mà AB - BD = AD
AC - CE = AE
=> AD = AE
Vì ΔHDE cân
=> H ∈ đường trung trực cạnh DE (1)
Xét ΔADHvàΔAEHcó
AD = AE (cmt)
AH (chung)
DH = HE (cmt)
Do đó: ΔADH=ΔAEH(c−c−c)
=> AD = AE ( hai cạnh tương ứng)
=> ΔADE cân tại A
=> A ∈ đường trung trực cạnh DE (2)
(1); (2) => A,H ∈ đường trung trực cạnh DE
=>AH là đường trung trực cạnh DE
CHÚC BẠN HỌC TỐT
bn j đó ơi cảm ơn bn đx giải cho mk nhung phần b) sai rồi nha
Cho tam giác ABC cân tại A, vẽ AH vuông góc BC
AB=10cm AH=8cm BH=6cm
So sánh các góc trong tam giác AHB?
\(\text{Xét }\Delta ABC\text{ có:}\)
\(AB>AH>BH\left(10cm>8cm>6cm\right)\)
\(\widehat{H}>\widehat{B}>\widehat{A\text{(quan hệ giữa cạnh và góc đối diện trong tam giác)}}\)
Bài 1: Cho tam giác ABC cân tại A. Vẽ AH vuông góc BC tại H
a/ Chứng minh tam giác AHB bằng tam giác AHC và BH = HC
b/ Cho biết AB = 13cm; BC = 10cm. Vẽ trung tuyến BM của tam giác ABC cắt AH tại G. Tính AH và AG.
c/ Vẽ trung tuyến CN của tam giác ABC. Chứng minh MN song song BC
d/ Trên cạnh AB lấy điểm D (D nằm giữa N và B) và trên tia đối tia CA lấy điểm E sao cho BD = CE. Đường thẳng qua C song song với DE và đường thẳng qua D song song với AC cắt nhau tại
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: BH=CH
b: Ta có: BH=CH
nên \(BH=CH=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
\(\Leftrightarrow AG=8\left(cm\right)\)
c: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC
Cho tam giác ABC cân tại A, vẽ AH vuông góc với BC tại H.Biết AB= 10cm, BH= 6cm.
a, Tính AH
b, tam giác ABH= tam giác ACH.
c, trên BA lấy D, CA lấy E sao cho BD= CE.Chứng minh tam giác HDE cân.
d, AH là trung trực của DE
a, AH= 8cm
vi ad la tia p/g cua bc => a1=a2
xet tg abh va tg ach co
ab=ac(gt) }
a1=a2 (gt) } gt ABH =TG ACH (C.GC)
ah canh chung }
c,vì abh = ach câu b =>hde cân
Cho tam giác ABC cân tại A có AB = 10cm, BH = 6cm. Vẽ AH vuông góc BC tại H.
a, Tính AH =?
b) Chứng minh tam giác ABH= tam giác ACH , từ đó chứng minh AH là tia phân giác của góc A.
c) Từ H vẽ HM vuông góc AB (M ϵ AB) và kẻ HN vuông góc AC (N ϵ AC) .
Chứng minh : tam giác BHM = tam giác HCN
d) Từ B kẻ Bx vuông góc AB, từ C kẻ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao?
CÁC BẠN VẼ HÌNH GIÚP MÌNH NHA! MÌNH CẢM ƠN CÁC BẠN! ![]()
a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O
Cho tam giác ABC cân tại A,vẽ BH vuông góc với AC (H thuộc AC). Tính AH, biết AB=15cm,BC=10cm.
Cái đề sai sai rồi...đấy ạ...?!!!
Cho tam giác ABC cân tại A, có AB = 10cm : BC= 16cm.Vẽ AH vuông góc BC tại A
a) CM ; tan giác HAB = tam giác HAC
b) CM: H là trung điểm BC. Tính AH
c) Vẽ HE vuông góc AB, HF vuông góc AC. CM ; tam giác HBE = tam giác HCF
d) CM; tam giác HAE = tam giác HAF và tam giác AEF cân
a) xét tg HAB và tg HAC có AB=AC(gt);góc AHB=góc AHC(=90 độ),chung AH
=>tg HAB và tg HAC bằng nhau (c.g.c)
b)=>HB=HC =>H là tđ BC. ta có tg ABH vuông tại H
=>AB^2=BH^2+AH^2 ( do H là tđ BC(cmt) vàBC=16cm(gt))+định lí pytago
hay 10^2=8^2+AH^2
AH^2=36
=> AH=6
c)có tg hab=tg hac=>bah=cah
xét tg eah và tg fah có: chung ah
bah=cah(cmt)
aeh=afh
=>tg eah=tg fah =>af=ae.MÀ ab=ac(gt)=>fc=be
=>tg hbe=tg hcf(c.g.c)
d)cmt.có af=fe(cmt)=>tgaef cân
k dúng mình cái mình làm bài này mệt lắm r
Cho tam giác ABC, biết AB = 6cm, BC = 10cm, AC = 8cm.
a) Chứng minh rằng tam giác ABC vuông
b) Vẽ AH vuông góc với BC tại H, phân giác góc CAH cắt BC tại D. CM: Tam giác ABD cân.
c) Vẽ DE vuông góc với AC tại E, trên tia AH lấy điểm M sao cho AM= AC. CMR: HE//MC
d) CMR: M, D, E thẳng hàng
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
1) Chứng minh tam giác ABH = tam giác ACH và H là trung điểm của BC.
2) Nếu có AB = 10cm, BC = 12 cm, hãy tính độ dài đoạn thẳng AH.
3) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Lấy các điểm M và N sao cho E là trung điểm của HM, F là trung điểm của HN. Chứng minh AN = AH.
4) Tam giác ABC cần thêm điều kiện gì thì A là trung điểm của MN?
Giúp mik vs ạ mik đang cần gấp.
1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
2: Ta có: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=64\)
=>\(HA=\sqrt{64}=8\left(cm\right)\)
3: Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AH
4: Xét ΔAHM có
AE là đường trung tuyến
AE là đường cao
Do đó: ΔAHM cân tại A
=>AM=AH
Ta có: ΔAHN cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAN
=>\(\widehat{HAN}=2\cdot\widehat{HAC}\)
Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
=>\(\widehat{HAM}=2\cdot\widehat{HAB}\)
Ta có: AM=AH
AH=AN
Do đó: AM=AN
Ta có: \(\widehat{HAM}+\widehat{HAN}=\widehat{MAN}\)
=>\(\widehat{MAN}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{MAN}=2\cdot\widehat{BAC}\)
Để A là trung điểm của MN thì AM=AN và góc MAN=180 độ
=>góc MAN=180 độ
=>\(2\cdot\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=90^0\)