đếm hộ nhé có bao nhiêu hình tam giác ko tính tam giác ghép
23. Có bao nhiêu hình tam giác?
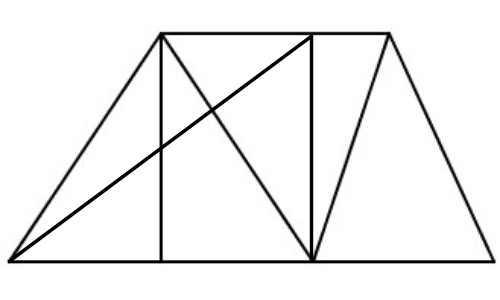
14
15
16
17
Giúp mik nhé chứ đếm nhẩm ko ra:))
a) Đếm số hình ghép thành bức tranh sau:
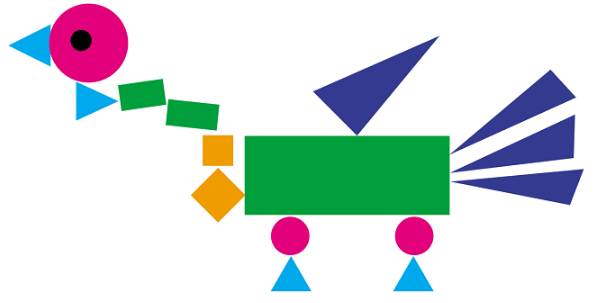 '
'
b) Bức tranh có bao nhiêu hình vuông? Hình tròn? Hình tam giác? Hình chữ nhật?
Các anh chị có thể giúp em đếm xem hình này có bao nhiêu hình tam giác được ko ạ?
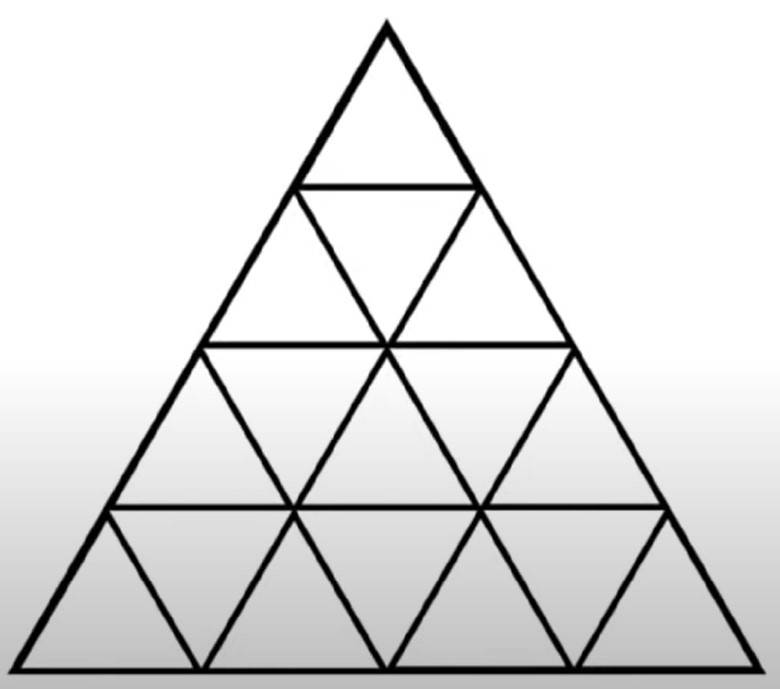
Có tổng cộng 27 hình tam giác.
Bài toán 'đếm số tam giác'
Từ 10 đoạn thẳng có độ dài tương ứng, có bao nhiêu cách để chọn ra 3 đoạn có thể ghép thành hình tam giác.
An có 10 đoạn thẳng có độ dài 1, 2, …, 10 đơn vị độ dài tương ứng. Hỏi có bao nhiêu cách khác nhau để chọn ra ba đoạn thẳng có thể tạo thành một tam giác.
Tất cả là 50 tam giác. Cách tính: tổng tổ hợp của 3 số trong 10 số trừ đi tổng tổ hợp của 3 trong 10 mà không thể thành tam giác. Cách tính hơi dài dòng nhưng có thể đúng giống như cách đếm đàn bò trong nông trại .
cho mình nha mình lại cho nhớ nha
Tổng 2 cạnh phải lớn hơn cạnh thứ 3! Suy ra:
Cạnh dài 1: không chọn được tam giác nào
Cạnh dài 2: 7 tam giác
Cạnh dài 3: 11 tg mới
Cạnh dài 4: 12 tg mới
Cạnh dài 5: 10 tg mới
Cạnh dài 6: 6 tg mới
Cạnh dài 7: 3 tg mới
Cạnh dài 8: 1 tg mới
Tổng cộng : 50 tam giác!
hình chũ nhật ABCDcó M là trung điểm của cạnh CD, chiều dài 32cm, chiều rộng 16cm.
a, trong hình bên có bao nhiêu hình tam giác.
b, tính diện tích hình thang ABCM
c, tính diện tích hình tam giác AMD
các bạn vẽ hình và giải hộ mình nhé, mình cảm ơn
Cho tam giác ABC có AB=3cm,AC=4cm,BC=5cm.
a)Chứng minh tam giác ABC là tam giác vuông
b)Trên tia đối của tia AB lấy điểm D sao cho AD=1cm. Tính CD
(GIẢI HỘ MÌNH CÂU b NHÉ , KO CẦN VẼ HÌNH ĐÂU)
Ta có
b) DC2=AC2+ AD2
=> DC2=16+1
=> DC2=17
VẬY DC=\(\sqrt{17}\)
hình vẽ này có bao nhiêu hình tam giác
hình tam giác gồm có 2 đường ngang và 3 nét kẻ dọc xuống
mình ko biết in hình nên các bạn tự đọc và tự hiểu cho mình nhé
Công thức tính số tam giác nếu đề bài cho n điểm không thẳng hàng, cứ 3 điểm ko thẳng hàng= 1 tam giác. Hỏi có bao nhiêu tam giác
Các bạn ghi cho mình công thức nhé
Công thức tính số tam giác nếu đề bài cho n điểm không thẳng hàng, cứ 3 điểm ko thẳng hàng= 1 tam giác. Hỏi có bao nhiêu tam giác:
Mình nghĩ là: \(\frac{n\left(n-1\right)}{2}\)
Cho đa giác n đỉnh (n>4)
a) Đếm số đường chéo của đa giác
b) Có bao nhiêu tam giác có đỉnh là đỉnh của đa giác
c) Có bao nhiêu tam giác có 2 cạnh là 2 cạnh của đa giác
d) Có bao nhiêu tam giác chỉ có 1 cạnh là cạnh của đa giác
e) Có bao nhiêu tam giác không có cạnh nào của đa giác
a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)