
Mình đang cần gấp !!! ( Mình cần lời giải chi tiết )
 Mình đang cần gấp và câu lời giải chi tiết ạ
Mình đang cần gấp và câu lời giải chi tiết ạ
Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.
mình cần lời giải chi tiết, đầy đủ aiiiiiiiiiiiiiiiiiii có thể giúp mình được ko vậy mình đang cần gấp ngay bây giờ nha mình cảm ơn
a/ Ta có: \(\begin{matrix}a\text{ // }b\\a\perp AB\end{matrix}\Rightarrow b\perp AB\)
b/ \(\hat{ACD}+\hat{CDB}=180^o\) (trong cùng phía, a // b)
\(\Rightarrow\hat{CDB}=180^o-\hat{ACD}=60^o\)
\(\hat{ACD}+\hat{aCD}=180^o\) (kề bù)
\(\Rightarrow\hat{aCD}=180^o-\hat{ACD}=60^o\)
Giúp mình mấy câu trong ảnh nhé 12,13,14,15,17,19,20,27,28,30. Mình đang cần gấp. Các bạn làm được câu nào thì giúp mình nhé. Mình chỉ cần đáp án thôi ko cần lời giải chi tiết.




Mọi người ơi giúp mình với. Please 🙏 mình cần gấp. Giúp mình thì mình giúp lại
260% của 25 kg là:
260 x 25 : 100 = 65(kg)
Đáp số: 65 (kg)
Tik mình nha!Cảm ơn!Học tốt
bài giải
260% của 25 là : 260 x 25 : 100 = 65(kg) ấn đúng nha.
Tìm n ∈ N để n5 + 1 chia hết cho n3 + 1 Mong đc câu trả lời chính xác và nhanh nhất ạ, giải chi tiết dùm mình nha Mình đang cần gấp, mình cảm ơn ạ, giải chi tiết dùm mình nha
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
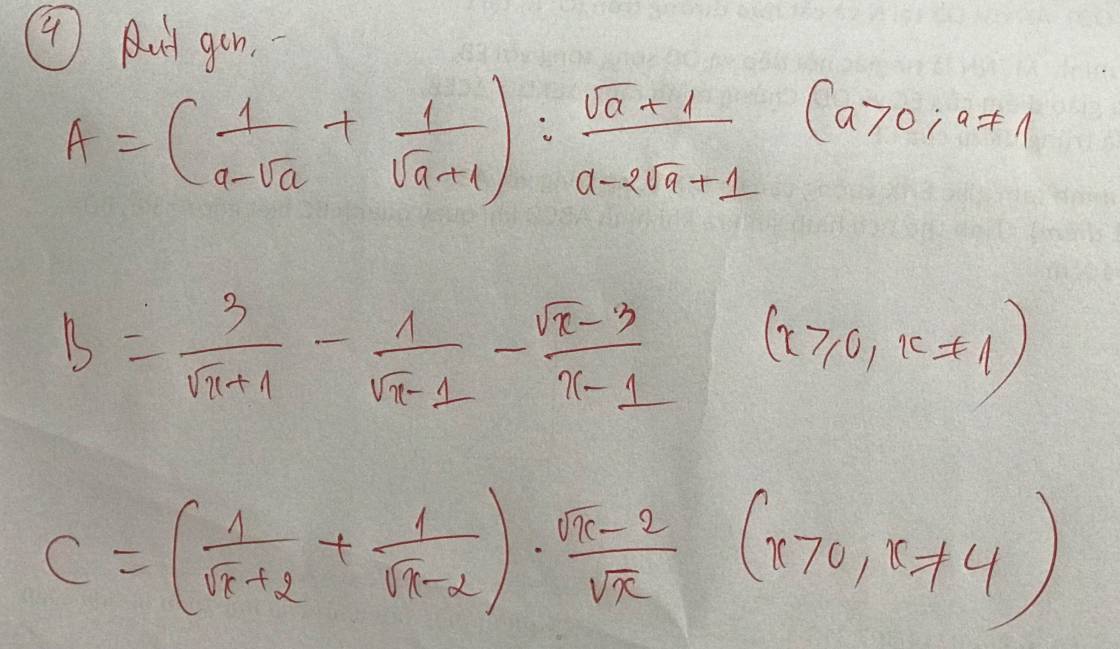 Cho mình câu trả lời chi tiết mình đang cần gấp
Cho mình câu trả lời chi tiết mình đang cần gấp
\(A=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}+1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\left(dkxd:a>0,a\ne1\right)\)
\(=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(a-\sqrt{a}\right)\left(\sqrt{a}+1\right)}.\dfrac{\sqrt{a^2}-2\sqrt{a}+1}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}.\dfrac{\left(\sqrt{a}-1\right)}{\sqrt{a}+1}\)
\(=\dfrac{1+a}{\sqrt{a}\left(\sqrt{a}+1\right)^2}\)
\(B=\dfrac{3}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\left(dkxd:x\ge0,x\ne1\right)\)
\(=\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{1+\sqrt{x}-3}{\sqrt{x}-1}\)
\(=\dfrac{3\sqrt{x}-3-\left(1+\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}+1}\)
\(C=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right).\dfrac{\sqrt{x}-2}{\sqrt{x}}\left(dkxd:x>0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}.\sqrt{x}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
a: \(A=\dfrac{\sqrt{a}+1+a-\sqrt{a}}{\left(\sqrt{a}+1\right)\cdot\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\)
\(=\dfrac{\left(a+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
b: \(B=\dfrac{3\sqrt{x}-3-\sqrt{x}-1-\sqrt{x}+3}{x-1}=\dfrac{\sqrt{x}-1}{x-1}\)
=1/(căn x+1)
c: \(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}+2}=\dfrac{2}{\sqrt{x}+2}\)
 Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!
Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!

Giúp mình giải chi tiết với mình đang cần gấp
\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)