a. Để đồ thị qua A

\(\Rightarrow-1=-3m+m-1\)

\(\Leftrightarrow m=0\)

b. Để đồ thị cắt trục tung tại điểm có tung độ 2

\(\Rightarrow m-1=2\)

\(\Leftrightarrow m=3\)

c. Để đồ thị cắt trục hoành tại điểm có hoành độ 3

\(\Rightarrow0=3m+m-1\)

\(\Leftrightarrow m=\dfrac{1}{4}\)

Chọn A.

Đồ thị hàm số có điểm cực tiểu khi và chỉ khi phương trình y’ = 0 có hai nghiệm phân biệt

Khi đó, giả sử x₁, x₂ là hai nghiệm của phương trình y’=0.

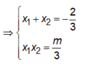
Bảng biến thiên

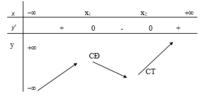
Do  nên hoặc nên điểm cực tiểu của đồ thị hàm số  nằm bên phải trục tung

(1),(2) => m < 0 

Đáp án là A

a) y=(m-1)x+m+3   (d1)  (a=m-1;b=m+3)

y=-2x+1  (d2)   (a' =-2;b' =1)

vì hàm số (d1) song song với hàm số  (d2) nên

\(\hept{\begin{cases}a=a'\\b\ne b'\end{cases}}\Leftrightarrow\hept{\begin{cases}m-1=-2\\m+3\ne1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}m=-1\\m\ne-2\end{cases}}\)

vậy với m= -1 thì hàm số  (d1)  song song với hàm số  (d2) 

b) vì hàm số (d1) đi qua điểm  (1;-4) nên 

x=1 ; y= -4

thay vào (d1) ta có 

-4=m-1+m+3        (mình làm tắt ko nhân với 1 nha)

-4=2m+2

-2=2m

m=-1

a, Để y là hàm số bậc nhất thì \(m+5\ne0\Leftrightarrow m\ne-5\)

b, Để y là hàm số đồng biến khi \(m+5>0\Leftrightarrow m>-5\)

c, Thay x = 2 ; y = 3 vào hàm số y ta được : 

\(2\left(m+5\right)+2m-10=3\)

\(\Leftrightarrow4m=3\Leftrightarrow m=\frac{3}{4}\)

d, Do đồ thị cắt trục tung tại điểm có hoành độ bằng 9 => y = 9 ; x = 0 

Thay x = 0 ; y = 9 vào hàm số y ta được : 

\(2m-10=9\Leftrightarrow m=\frac{19}{2}\)

e, Do đồ thị đi qua điểm 10 trên trục hoành => x = 10 ; y = 0 

Thay x = 10 ; y = 0 vào hàm số y ta được : 

\(10m+50+2m-10=0\Leftrightarrow12m=-40\Leftrightarrow m=-\frac{40}{12}=-\frac{10}{3}\)

f, Ta có : y = ( m + 5 )x + 2m -  10 => a = m + 5 ; b = 2m - 10 ( d1 ) 

y = 2x - 1 => a = 2 ; y = -1 ( d2 ) 

Để ( d1 ) // ( d2 ) \(\Rightarrow\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}\Leftrightarrow\hept{\begin{cases}m=-3\\2m\ne9\end{cases}\Leftrightarrow}\hept{\begin{cases}m=-3\left(tm\right)\\m\ne\frac{9}{2}\end{cases}}}\)

g, h cái này mình quên rồi, xin lỗi )): 

Xét \(M\left(0;m\right)\in Oy\), đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)

d là tiếp tuyến \(\Leftrightarrow\begin{cases}\frac{x+1}{x-1}=kx+m\\\frac{-2}{\left(x-1\right)^2}=k\end{cases}\) có nghiệm

Thế k vào phương trình thứ nhất, ta được :

\(\frac{x+1}{x-1}=\frac{-2x}{\left(x-1\right)^2}+m\Leftrightarrow\left(m-1\right)x^2-2\left(m+1\right)x+m+1=0\) (*)

Để từ M chỉ kẻ được đúng một tiếp tuyến đến đồ thị hàm số đã cho \(\Leftrightarrow\) (*) có đúng 1 nghiệm. 

Do (*) không có nghiêm x = 1 nên (*) có đúng 1 nghiệm

\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\\Delta'=2m+2=0\end{array}\right.\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}m=1\\m=-1\end{array}\right.\)

Vậy có 2 điểm \(M_1\left(0;1\right);M_2\left(0;-1\right)\) thỏa mãn bài toán

Đáp án A