Các câu hỏi tương tự
Cho hàm số
y
x
3
+
(
m
+
3
)
x
2
-
(
2
m
+
9
)
x
+
m
+
6
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất. A. m
-...
Đọc tiếp
Cho hàm số y = x 3 + ( m + 3 ) x 2 - ( 2 m + 9 ) x + m + 6 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất.
A. m = - 6 ± 3 2 2
B. m = - 3 ± 3 2 2
C. m = - 3 ± 6 2
D. m = - 6 ± 6 2
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
y
2
x
3
-
3
(
m
+
1
)
x
2
+
6
m
x
có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng
d
:
y
x
+
2
Số phần tử của S là A. 0 B. 1 C...
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Cho hàm số
y
x
3
-
3
m
x
2
+
2
(
m
2
-
1
)
x
-
m
3
-
m
(m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằ...
Đọc tiếp
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
f
x
+
m
có 5 điểm cực trị. A.
m
≤
−
1
B.
m
−
1
C.
m
≥
−
1
D.
m
−...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
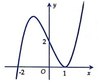
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > − 1
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
f
x
+
m
có 5 điểm cực trị. A.
m
≤
−
1
B.
m
−
1
C.
m
≥
−
1
D.
m
1
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
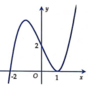
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > 1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
1
3
x
3
−
m
−
1
x
2
+
1
−
3
m
có 2 điểm cực trị A, B sao cho A, B và
C
0
;
−
5
thẳng hàn...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 1 3 x 3 − m − 1 x 2 + 1 − 3 m có 2 điểm cực trị A, B sao cho A, B và C 0 ; − 5 thẳng hàng ?
A. m = 1
B. m = 2
C. 1 ≠ m ≤ 2
D. 1 < m ≤ 2
Cho hàm số yf(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số
h
(
x
)
f
2
(
x
)
+
f
(
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số h ( x ) = f 2 ( x ) + f ( x ) + m có đúng 3 điểm cực trị.
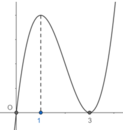
A. m ≤ 1
B. m > 1 4
C.m<1
D. m ≥ 1 4
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
−
3
x
2
−
m
x
+
2
có hai điểm cực trị A và B sao cho các điểm A, B và M(0;3) thẳng hàng. A. m -3 B. Không tồn tại m C.
m
−
2
D. m 3
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 − 3 x 2 − m x + 2 có hai điểm cực trị A và B sao cho các điểm A, B và M(0;3) thẳng hàng.
A. m = -3
B. Không tồn tại m
C. m = − 2
D. m = 3
Cho hàm số
y
2
x
3
-
3
m
2
-
m
+
1
x
2
+
6
m
2
-
6
m
x
, với m là tham số. Gọi S là t...
Đọc tiếp
Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4




