Cho tam giác ABC.Gọi M,N lần lượt là trung điểm của AB,AC.Chứng minh:MN//BC
MN=1/2 BC (có vẽ hình)
cho tam giác ABC.Gọi M,N lần lượt là trung điểm của các cạnh AB và AC.Chứng minh:MN song song BC;MN=BC/2
vì M là TĐ của AB,N là tđ của ac nên:
→MN là đg trung bình của tam giác AbC
→MN //BC,MN=1/2 BC
theo mh nghĩ là vậy.sai thì đừng trách nhé!
Cho tam giác ABC(AB<AC) có đường cao AH. Gọi M, N, K lần lượt là trung điểm của AB, AC, BC. a) CMR tứ giác BCMN là hình thang
b) Chứng minh tứ giác AMKN là hình bình hành
c) Gọi D là điểm đối xứng của H qua M. Chứng minh ADBH là hình chữ nhật
d) Tìm điều kiện của tam giác ABC để AMKN là hình vuông
Cho tam giác ABC gọi M,N,P lần lượt là trung điểm của BC,AB,AC.Chứng minh MNAP là hình bình hành
GIÚP MK VẼ HÌNH VÀ GT,KL NHA MAI TUI KIỂM TRA RÙI
Bạn thông cảm, mk ko bít vẽ hình trên olm
Xét tam giác ABC có M,P lần lượt là trung điểm của BC,AC (gt)
=> MP là đường trung bình của tam giác ABC
=> MP // AB mà N thuộc AB
=> MP // NA (1)
Tương tự MN //AP (2)
Từ 1, 2 =. tứ giác MNAP là hình bình hành
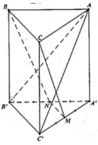
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M và N lần lượt là trung điểm của A’C’ và A’B’ (như hình vẽ bên). Tính cosin của góc tạo bởi hai mặt phẳng (AB’C’) và (BCMN).
A. 13 65
B. 13 130
C. - 13 130
D. - 13 65
cho tam giác ABC vuông tại A có M,N,P lần lượt là trung điểm của AB,BC,AC.Chứng minh tứ giác MNCA là hình thang vuông.chứng minh tứ giác MNPA là hinhf bình hanhf
Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm của AB và AC.
Chứng minh rằng:
a)MN//BC
b)BN=CM
Giúp mik với .Có Vẽ hình nha bạn;)
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔABC có
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
Do đó: MN//BC
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{A}\) chung
BN=CM
Do đó: ΔABN=ΔACM
a)M,N là trung điểm AB,AC
\(\Rightarrow MN\) là đường trung bình
\(\Rightarrow MN//BC\)
b) M là trung điểm \(AB\Rightarrow MB=\dfrac{AB}{2}màAB=AC\)
N_____\(AC\Rightarrow NC=\dfrac{AC}{2}\Rightarrow MB=NC\)
\(BNC=CMB\left(C-g-c\right)\Rightarrow CM=BN\)
Cho tam giác ABC cân tại A ,lấy M,N lần lượt là trung điểm của AB,AC.Chứng minh MN//BC,MN=1/2BC
Lời giải:
Tam giác $ABC$ cân tại $A$ nên:
$\widehat{ABC}=\frac{180^0-\widehat{A}}{2}$
$M,N$ là trung điểm của $AB,AC$ mà $AB=AC$ nên $AM=AN$
$\Rightarrow \triangle AMN$ cân tại $A$
$\Rightarrow \widehat{AMN}=\frac{180^0-\widehat{A}}{2}$
Do đó: $\widehat{ABC}=\widehat{AMN}$
$\Rightarrow MN\parallel BC$
Trên tia đối của tia $NM$ lấy $P$ sao cho $NM=NP$
Dễ chứng minh $\triangle AMN=\triangle CPN$ (c.g.c)
$\Rightarrow \widehat{AMN}=\widehat{CPN}$ $\Rightarrow AM\parallel CP$
$\Rightarrow BM\parallel CP$
$\Rightarrow \widehat{BMC}=\widehat{PCM}$ (so le trong)
Xét tam giác $BMC$ và $PCM$ có:
$MC$ chung
$\widehat{BMC}=\widehat{PCM}$ (cmt)
$\widehat{BCM}=\widehat{PMC}$ (so le trong)
$\Rightarrow \triangle BMC=\triangle PCM$ (g.c.g)
$\Rightarrow BC=PM=2MN\Rightarrow MN=\frac{BC}{2}$
Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: MN//BC và \(MN=\dfrac{1}{2}\cdot BC\)(Định lí 2 về đường trung bình của tam giác)
Cho tam giác ABC. Gọi N,M lần lượt là trung điểm của AB,AC
a) Chứng minh rằng: Tứ giác BCMN là hình thang
b)Tìm điều kiện của tam giác ABC để tứ giác BCMN là hình thang cân.Chứng minh.
a) dùng đường trung bình của tam giác
b) Để BCMN là hình thang cân thì \(\widehat{A}=\widehat{B}\)
=> \(\Delta ABC\)cân tại A
Mình làm tắt, bạn tự trình bày đầy đủ nhé
a) dùng đường trung bình của tam giác
b) Để BCMN là hình thang cân thì ^A=^B
=> ΔABC cân tại A
câu hỏi hay......nhưng tui xin nhường cho các bn khác
Hãy tích đúng cho tui nha
THANKS
Câu 1:
Cho tam giác ABC có AB=AC>BC
Gọi M,N lần lượt là trung điểm của AC,AB
Lấy điểm D sao cho M là trung điểm của ND
Tia AD cắt BC kéo dài tại E
a) Chứng minh tam giác AMN = tam giác CMD và AB//CD
b) Chứng minh tam giác NCB = tam giác CND và DN//BE
c) Chứng minh BCMN là hình thang cân và ANCE là hình thang
d) So sánh BD và NE
a) Xét tam giác AMN và tam giác CMD có:
MN = MD ( M là trung điểm của ND)
Góc NMA = góc DMC ( đối đỉnh)
MA = MC ( M là trung điểm của AC )
=> tam giác AMN = tam giác CMD ( c-g-c)
=> Góc NAM = góc DCM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong => AN//DC=> AB//DC ( vì A, N, B là 3 điểm tạo nên cùng 1 đường thẳng).
b) Ta có: AN = DC ( tam giác AMN = tam giác CMD)
Mà AN = NB ( N là trung điểm của AB)
=> DC = NB
Xét tam giác NCB và tam giác CND có:
NC là cạnh chung
Góc BNC = góc DCN( so le trong, NB//DC)
NB = DC (cmt)
=> tam giác NCB = tam giác CND ( c-g-c)
=> Góc BCN = góc DNC ( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong => ND//BC=> ND//BE
c) Ta có: ND//BE(cmt)=> NM//BC=> BCMN là hình thang (1)
Ta có: AB = AC (gt)
=> Góc ABC = góc ACB ( quan hệ giữa góc và cạnh đối diện)
=> Góc NBC = góc MCB (2)
Từ (1) và (2) => BCMN là hình thang cân
Xét tam giác AMD và tam giác CMN có:
MA = MC ( M là trung điểm của cạnh AC)
Góc DMA = góc NMC ( đối đỉnh)
MN = MD ( M là trung điểm của cạnh ND)
=> Tam giác AMD = tam giác CMN (c-g-c)
=> Góc DAM = góc NCM ( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong => AE//NC => ANCE là hình thang
d) BD>NE