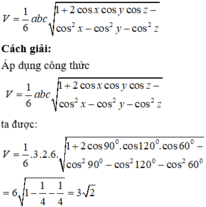Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^o\) ; \(\widehat{CAD}=90^o\).
Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB và IJ.
Những câu hỏi liên quan
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)
\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)
Đúng 1
Bình luận (0)
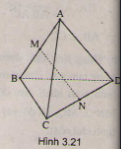
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^0\). Chứng minh rằng :
a) \(AB\perp CD\)
b) Nếu M, N lần lượt là trung điểm của AB và CD thì \(MN\perp AB\) và \(MN\perp CD\)
Hướng dẫn.
(h.3.21)
a)
Suy ra
Ta có => AB ⊥ MN.
Chứng minh tương tự được CD ⊥ MN.
Đúng 0
Bình luận (0)
1/cho tứ giá lồi ABCD có AB=BC=CD=a , \(\widehat{BAD}=75^o,\widehat{ADC}=45^o\).tính AD
2/cho tứ giác ABCD có\(AB-6\sqrt{3},CD=12,\widehat{A}=60^o,\widehat{B}=150^o,\widehat{D}=90^o\). tính BC
Tứ giác ABCD có AB = AD, \(\widehat{BAD}=60^o,\widehat{BCD}=120^o\). Chứng minh CA = CB + CD
Trên tia đối của DC lấy I sao cho DI = CB
Khi đó: \(CB+CD=DI+CD=IC\)
Tứ giác ABCD có: \(\widehat{BAD}+\widehat{BCD}=60^0+120^0=180^0\)
\(\Rightarrow\widehat{ADC}+\widehat{ABC}=180^0\)
Mà \(\widehat{ADC}+\widehat{ADI}=180^0\Rightarrow\widehat{ABC}=\widehat{ADI}\)
\(\Delta BAD:AB=AD,\widehat{BAD}=60^0\Rightarrow\Delta BAD\) đều
\(\Rightarrow\widehat{BAD}=60^0\)
\(\Delta ABC=\Delta ADI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}\widehat{BAC}=\widehat{DAI}\\AC=AI\end{cases}}\)
\(\widehat{CAI}=\widehat{CAD}+\widehat{DAI}=\widehat{CAD}+\widehat{BAC}=\widehat{BAD}=60^0\)
Tam giác ACI đều nên AC = AI = CI
Mà \(CB+CD=IC\Rightarrow CA=CB+CD\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
A
C
A
D
và
B
A
C
^
B
A
D
^
60
°
. Xác định góc giữa hai đường thẳng AB và CD A.
90
°
B...
Đọc tiếp
Cho tứ diện ABCD có A B = A C = A D và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Cho tứ diện ABCD có ABACAD và
B
A
C
^
B
A
D
^
60
°
. Xác định góc giữa hai đường thẳng AB và CD
Đọc tiếp
Cho tứ diện ABCD có AB=AC=AD và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
Cho tứ diện ABCD có AB AC AD a và
B
A
C
^
B
A
D
^
60
°
. Hãy xác định góc giữa cặp vectơ
A
B
→
,
C
D
→
A.
60
°
B.
45
°
C. ...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = a và B A C ^ = B A D ^ = 60 ° . Hãy xác định góc giữa cặp vectơ A B → , C D →
A. 60 °
B. 45 °
C. 120 °
D. 90 °
Cho tứ diện ABCD có AB 3, AC 2, AD 6,
B
A
C
^
90
°
,
C
A
D
^
120
°
,
B
A
D
^
...
Đọc tiếp
Cho tứ diện ABCD có AB = 3, AC = 2, AD = 6, B A C ^ = 90 ° , C A D ^ = 120 ° , B A D ^ = 60 ° . Thể tích khối tứ diện ABCD bằng
A. 6 2
B. 2 2 3
C. 2
D. 3 2
Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
Đúng 0
Bình luận (0)