Đề thiếu. Ghi thế này ai hiểu?

a) Vì cứ qua 2 điểm ta kẻ được 1 và chỉ 1 đường thẳng . Nếu có 2 điểm thẳng hàng , từ 1 điểm kẻ lần lượt với 10 điểm còn lại ta được:

11 . 10 = 110 ( đường thẳng ) . Nhưng như vậy mỗi đường thẳng được tính hai lần nên có số đường thẳng là :

   110 : 2 = 55 ( đường thẳng )

b) Vì cứ qua 2 điểm ta kẻ được 1 và chỉ 1 đường thẳng .Nếu có 2 điểm thẳng hàng  từ 1 điểm kẻ lần lượt với 10 điểm còn lại ta được:

11 . 10 = 110 ( đường thẳng ) . Nhưng như vậy mỗi đường thẳng được tính hai lần nên có số đường thẳng là :

   110 : 2 = 55 ( đường thẳng )

 + Nếu có 5 điểm không thẳng hàng , từ 1 điểm kẻ được với 4 điểm còn lại  làm như vậy với 5 điểm ta có : 4 . 5 = 20 ( đường thẳng )

Nhưng vì có điểm thẳng hàng nên 20 đường thẳng này chỉ được tính là 1

  Vậy số đường thẳng kẻ được trong đó có 5 điểm thẳng hàng là :

    55 - 20 + 1 = 36 ( đường thẳng )

a) Ta có: ID vuông góc AM với D là trung điểm AM => ID là đường trung trực AM => IA = IM (1)

IE vuông góc AN với E là trung điểm AN => IE là đường trung trực AN => IA = IN (2)

Từ (1) và (2) => IA = IM = IN

=> I là tâm đường tròn qua 3 điểm A; M; N

b. Lấy điểm P đối xứng với điểm A qua BC => P cố định

=> BC là đường trung trực của PA mà I thuộc BC 

=> IP = IA 

=>( I) qua điểm P cố định khác A

Để vẽ được các đường thẳng như yêu cầu, chúng ta có thể sử dụng nguyên tắc "mỗi đường thẳng đi qua 2 trong 4 điểm trên".

a. Để vẽ 6 đường thẳng, ta có thể chọn 2 điểm từ 4 điểm trên và vẽ đường thẳng đi qua chúng. Vì có 4 điểm, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 6 đường thẳng.

b. Tương tự, để vẽ 4 đường thẳng, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 4 đường thẳng.

c. Để vẽ 2 đường thẳng, ta cũng có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 2 đường thẳng.

Với các yêu cầu trên, chúng ta có thể vẽ được số đường thẳng tương ứng.

a, 6 đường thẳng

b, 28 đường thẳng

c, \(\frac{n.\left(n-1\right)}{2}\)đường thẳng

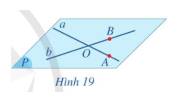
a) Mặt phẳng đi qua ba điểm A. B, O đi qua hai đường thẳng a và b

b) Có một và chỉ một mặt phẳng đi qua hai đường thẳng a và b

Huy làm có gì sai mọi người góp ý nha :3

a

Ta có 2 đường trung trực của các đoạn thẳng AM,AN cắt nhau tại I nên I là tâm đường tròn ngoại tiếp tam giác AMN

b

Hạ đường cao AK. Gọi L đối xứng với A qua K. Suy ra L cố định.Ta sẽ chứng minh tứ giác AMLN nội tiếp. Thật vậy !

Ta dễ có được đường tròn tâm I ngoại tiếp tam giác ALN 

Ta có:\(\widehat{AIN}=2\widehat{ALN};\widehat{AIN}=2\widehat{AMN}\Rightarrow\widehat{ALN}=\widehat{AMN}\) nên tứ giác AMLN nội tiếp khi đó đường tròn I luôn đi qua điểm L cố định

Hình tui đã vẽ trong TKHĐ nhé :))

Mình làm ra vở cho bạn rồi nhé. Chữ mình hơi xấu, mong bạn thông cảm.

Xin lỗi bạn nhiều lắm, vừa nãy mình gửi thiếu ảnh.