Trên nửa mặt phẳng bờ là NF, dựng tam giác đều NFG. Nối G với A và H.

Ta có: ^CFN + ^AFN = 60⁰; ^AFG + ^AFN = 60⁰ => ^CFN = ^AFG.

Xét \(\Delta\)NFC và \(\Delta\)GFA có: FC=FA;  ^CFN=^AFG; FN=FG => \(\Delta\)NFC = \(\Delta\)GFA (c.g.c)

=> CN=AG (2 cạnh tương ứng) . Mà CN=BN nên BN=AG.

Lại có: \(\Delta\)ABE là tam giác đều với trực tâm H => ^ABH=30⁰

=> ^HBN = ^ABC + ^ABH = ^ABC +30⁰ (1)

^HAG = 360⁰ - (^FAG + ^FAC + ^BAC + ^HAB) (*)

Do \(\Delta\)NFC=\(\Delta\)GFA => ^FAG = ^FCN (2 góc tương ứng) => ^FAG = ^ACB +60⁰

Dễ thấy: \(\Delta\)ACF đều => ^FAC = 60⁰;   \(\Delta\)ABE đều, trực tâm H => ^HAB = ^ABH = 30⁰

Thay hết vào (*), ta được: ^HAG = 360⁰ - (^ACB + 60⁰ + 60⁰ + ^BAC + 30⁰)

=> ^HAG = 210⁰ - (^BAC + ^ACB) = 180⁰ - (^BAC + ^ACB) +30⁰ = ^ABC + 30⁰

=> ^HAG = ^ABC + 30⁰ (2)

Từ (1) và (2) => ^HBN = ^HAG. 

Xét \(\Delta\)BHN và \(\Delta\)AHG có: BH=AH (Dễ c/m); ^HBN = ^HAG; BN=AG (cmt)

=> \(\Delta\)BHN=\(\Delta\)AHG (c.g.c) => HN=HG (2 cạnh tương ứng).

Xét \(\Delta\)HNF và \(\Delta\)HGF: GN=HG; FN=FG; HF chung => \(\Delta\)HNF=\(\Delta\)HGF (c.c.c)

=> ^HFG = ^HFN = ^GFN/2 = 60⁰/2 = 30⁰; ^NHF = ^GHF

\(\Delta\)BHN=\(\Delta\)AHG => ^BHN = ^AHG . Mà ^BHN + ^NHA = ^BHA = 120⁰

=> ^AHG + ^NHA = ^NHG = 120⁰ => ^NHF = ^GHF = ^NHG/2 = 60⁰

Vậy \(\Delta\)FNH có: ^HFN = 30⁰; ^NHF = 60⁰ =>  ^FNH = 90⁰.

Còn 1 cách khác ở trong sách Nâng cao phát triển Toán 7 - T2 nhé!

Mình nghĩ thêm cách này để bạn tham khảo ^-^

Cho cái link này không bít có đúng không:

https://cunghoctot.vn/forum/topic/1003161

Chia ra 3 trường hợp .....

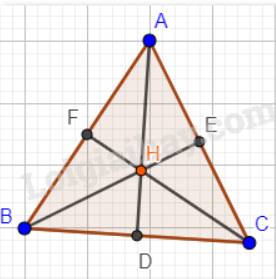
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.

Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.

Suy ra: AF = BF = AE = CE = BD = CD;

\(AD \bot BC; BE \bot AC; CF \bot AB\)

Xét tam giác ADB và tam giác ADC có:

     AD chung

    \(\widehat{ADB}=\widehat{ADC} (=90^0)\)

     BD = CD (D là trung điểm của đoạn thẳng BC).

Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).

Tương tự, ta cũng được, AC = BC

Xét tam giác ABC có AB = AC = BC nên là tam giác đều.

Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.

b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.

c)

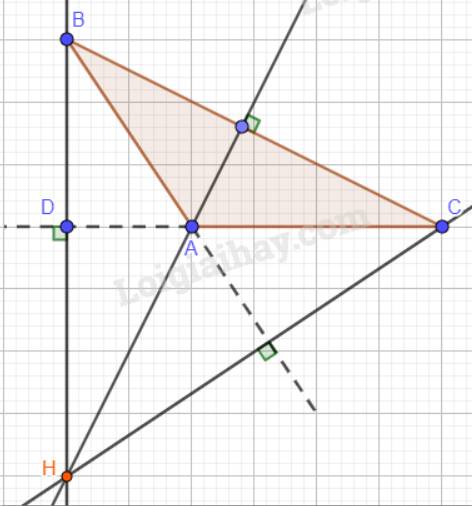
Nhận xét: H nằm ngoài tam giác ABC.

Tọa độ điểm C:

\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)

Ta có: 

\(\overrightarrow{AH}=\left(a-3;b+1\right)\)

\(\overrightarrow{BH}=\left(a+1;b-2\right)\)

\(\overrightarrow{BC}=\left(2;-6\right)\)

\(\overrightarrow{AC}=\left(-2;-3\right)\)

Theo giả thiết 

\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)

\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)

Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)

a: A(3;1); B(2;6); C(4;-1)

\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)

\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)

\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)

Chu vi tam giác ABC là:

\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)

b: Xét ΔABC có 

\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)

=>\(\widehat{A}\simeq165^0\)

c: Gọi H(x,y) là trực tâm của ΔABC

\(\overrightarrow{AH}=\left(x-3;y-1\right)\)

\(\overrightarrow{BH}=\left(x-2;y-6\right)\)

\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)

H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC

=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)

a: OM//AH

ON//BH

MN//AB

=>góc BAH=góc OMN và góc ABH=góc ONM

=>ΔABH đồng dạng với ΔMNO

b: A,G,M thẳng hàng và H,G,O thẳng hàng

=>góc AGH=góc MGO

=>ΔAHG đồng dạng với ΔMOG

=>OM/AH=MG/AG

=>OM/AH=MN/AB=1/2

=>GM/GA=1/2

=>G là trọng tâm của ΔACB

a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân

=> Loại

b: Gọi giao điểm của BH và AC là K

=> BK\(\perp\)AC tại K

Ta có: ΔABK vuông tại K

nên \(\widehat{ABK}+\widehat{BAK}=90^0\)

hay \(\widehat{BAC}=60^0\)

Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)

nên ΔABC đều

Ta có:

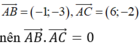
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A

Vậy H( -1 ; 3)

Chọn B.