+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)

góc A₂ = xAC / 2 

=> góc A₂ = (góc ABC + C1) / 2 = B₁ + ( C₁ / 2 ) (Vì góc B₁ = ABC /2 )

+) Trong tam giác AIB: góc AIB = 180^o - (B₁ + A₁  + A₂)

                                              = 180^o - (B₁ + A₁  +B₁ + ( C₁ / 2 ) )

                                              = 180^o - (2.B₁ + A₁  + ( C₁ / 2 ) )

                                              = 180^o - (B + A₁ + ( C₁ / 2 ))

Mà B + A₁ = 180^o - C₁ =  180^o - 70^o = 110^o; C₁ / 2 = 70^o/ 2 = 35^o

=> góc AIB = 180^o - (110^o + 35^o) = 180^o - 145^o = 35^o

Trần thị Loan là thành viên trong Online Math

+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)

góc A₂ = xAC / 2 

=> góc A₂ = (góc ABC + C1) / 2 = B₁ + ( C₁ / 2 ) (Vì góc B₁ = ABC /2 )

+) Trong tam giác AIB: góc AIB = 180^o - (B₁ + A₁  + A₂)

                                              = 180^o - (B₁ + A₁  +B₁ + ( C₁ / 2 ) )

                                              = 180^o - (2.B₁ + A₁  + ( C₁ / 2 ) )

                                              = 180^o - (B + A₁ + ( C₁ / 2 ))

Mà B + A₁ = 180^o - C₁ =  180^o - 70^o = 110^o; C₁ / 2 = 70^o/ 2 = 35^o

=> góc AIB = 180^o - (110^o + 35^o) = 180^o - 145^o = 35^o

Ve giup minh ca hinh voi minh can cuc gap

sai đề à

sai de

um sai đề rồi

a: Xét ΔBAD vuông tại A và ΔBKD vuông tại K có

BD chung

\(\widehat{ABD}=\widehat{KBD}\)

Do đó: ΔBAD=ΔBKD

b: Xét ΔADI vuông tại A và ΔKDC vuông tại K có

DA=DK

\(\widehat{ADI}=\widehat{KDC}\)

Do đó: ΔADI=ΔKDC

Suy ra: AI=KC

c: Ta có: BA+AI=BI

BK+KC=BC

mà BA=BK

và AI=KC

nên BI=BC

=>ΔBIC cân tại B

mà \(\widehat{IBC}=60^0\)

nên ΔBIC đều

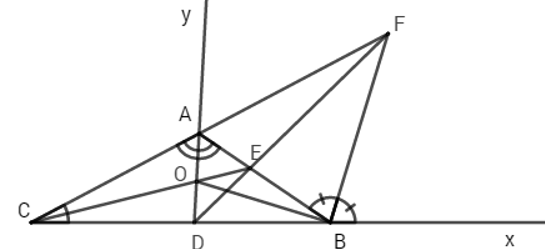
a) Xét   \(\Delta ABC\) có tia phân giác \(BAC,ACB\)  cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\)   (tính chất 3 đường phân giác của tam giác)

\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )

Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)

( tính chất của tia phân giác ) 

Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)

Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)

b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)

\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\)  ( dấu hiệu nhận biết tia phân  giác )

\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )

\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )

Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )

c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng