a) ( 2 + 1 )x = 45

        3x = 45

         x = 45 : 3

         x = 15

b) ( 2 + 7 )x = 918

           9x = 918

             x = 918 : 9

             x = 102

c) ( 2 + 3 )x = 65

           5x = 65

             x = 65 : 5

            x = 13

d) ( 11 + 22 )x = 66

          33 x = 66

                x = 66 : 33

               x = 2

a, 2x+x=45

   2x+x.1=45

   (2+1)x=45

      3x    =45

        x    =45:3

       x    = 15

Vậy...

Phần b xíu chirsau đc ko

a) 2x+x=45

    3x     =45

      x     =45:3

      x     =15

vậy... 

b) 2x+7x=918

    9x       =918

      x       =918:9

      x       =102

vậy...

c) 2x+3x=60+5

    5x      =65

      x       =65:5

      x       =13

vậy...

d)11x+22x=33.2

    33x       =66

        x       =66:33

        x       =22

vậy...

\(\dfrac{3-3x}{2x}+\dfrac{3x-1}{2x-1}+\dfrac{11x-5}{2x-4x^2}\\ =\dfrac{\left(3-3x\right)\left(1-2x\right)}{2x\left(1-2x\right)}-\dfrac{2x\left(3x-1\right)}{2x\left(1-2x\right)}+\dfrac{11x-5}{2x\left(1-2x\right)}\\ =\dfrac{3-9x+6x^2}{2x\left(1-2x\right)}-\dfrac{6x^2-2x}{2x\left(1-2x\right)}+\dfrac{11x-5}{2x\left(1-2x\right)}\\ =\dfrac{3-9x+6x^2-6x^2+2x+11x-5}{2x\left(1-2x\right)}\\ =\dfrac{-2}{2x\left(1-2x\right)}\\ =\dfrac{-1}{x\left(1-2x\right)}\)

a) 2x-7=11x+11

<=> 2x-11x=11+7

<=> -9x=17

<=> x= -17/9

b) 2011x -4 =x+6

<=> 2011x-x=6+4

<=> 2010x=10

<=> x=10/2010

<=> x=1/201

c) 5(2x-3)-2(3x-5)=0

<=> 10x-15-6x+10=0

<=> 10x-6x=15-10

<=>4x=5

<=> x=5/4

a)A=4(x+11/8)^2 -153/16

Min A=-153/16 khi x=-11/8

b)B=3(x-1/3)^2 -4/3

Min B=-4/3 khi x=1/3

Bài 1:

a) \(A=4x^2+11x-2=\left(4x^2+11x+\dfrac{121}{16}\right)-\dfrac{153}{16}=\left(2x+\dfrac{11}{4}\right)^2-\dfrac{153}{16}\ge-\dfrac{153}{16}\)

\(minA=-\dfrac{153}{16}\Leftrightarrow x=-\dfrac{11}{8}\)

b) \(B=3x^2-2x-1=3\left(x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x-\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\)

\(minB=-\dfrac{4}{3}\Leftrightarrow x=\dfrac{1}{3}\)

Bài 2:

a) \(A=-x^2+3x-1=-\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{5}{4}=-\left(x-\dfrac{3}{2}\right)^2+\dfrac{5}{4}\le\dfrac{5}{4}\)

\(maxA=\dfrac{5}{4}\Leftrightarrow x=\dfrac{3}{2}\)

b) \(B=-x^2-4x+7=-\left(x^2+4x+4\right)+11=-\left(x+2\right)^2+11\le11\)

\(maxB=11\Leftrightarrow x=-2\)

Bài 1: 

a: Ta có: \(A=4x^2+11x-2\)

\(=4\left(x^2+\dfrac{11}{4}x-\dfrac{1}{2}\right)\)

\(=4\left(x^2+2\cdot x\cdot\dfrac{11}{8}+\dfrac{121}{64}-\dfrac{153}{64}\right)\)

\(=4\left(x+\dfrac{11}{8}\right)^2-\dfrac{153}{16}\ge-\dfrac{153}{16}\forall x\)

Dấu '=' xảy ra khi \(x=-\dfrac{11}{8}\)

b: Ta có: \(B=3x^2-2x-1\)

\(=3\left(x^2-\dfrac{2}{3}x-\dfrac{1}{3}\right)\)

\(=3\left(x^2-2\cdot x\cdot\dfrac{1}{3}+\dfrac{1}{9}-\dfrac{4}{9}\right)\)

\(=3\left(x-\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{3}\)

a) 2x - x³ + 4y - 8y³

= ( 2x + 4y ) - ( x³ + 8y³ )

= 2( x + 2y ) - ( x + 2y )( x² - 2xy + 4y² )

= ( x + 2y )( 2 - x² + 2xy - 4y² )

b) -3x² + 11x + 14

= -3x² + 14x - 3x + 14

= -x( 3x - 14 ) - ( 3x - 14 )

= ( 3x - 14 )( -x - 1 )

1: \(\dfrac{2x^3+11x^2+18x-3}{2x+3}\)

\(=\dfrac{2x^3+3x^2+8x^2+12x+6x+9-12}{2x+3}\)

\(=x^2+4x+3-\dfrac{12}{2x+3}\)

a) \(\left(2x+3\right)^3=\left(2x+3\right)^8\)

\(\left(2x+3\right)^8-\left(2x+3\right)^3=0\)

\(\left(2x+3\right)^3.\text{ }\left[\left(2x+3\right)^5-1\right]=0\)

\(\Rightarrow\orbr{\begin{cases}\left(2x+3\right)^3=0\\\left(2x+3\right)^5-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2x+3=0\\\left(2x+3\right)^5=1\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{3}{2}\\x=-1\end{cases}}}\)

Vậy \(x=-\frac{3}{2}\) hoặc \(x=-1\)

Câu b tương tự

c) \(\left|5-3x\right|=\left|11x+2\right|\)

\(\Rightarrow\orbr{\begin{cases}5-3x=11x+2\\5-3x=-11x-2\end{cases}\Leftrightarrow\orbr{\begin{cases}11x+3x=2-5\\-3x+11x=-2+5\end{cases}\Leftrightarrow\orbr{\begin{cases}14x=-3\\8x=3\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{3}{14}\\x=\frac{3}{8}\end{cases}}}}\)

Vậy \(x=-\frac{3}{14}\)hoặc \(x=\frac{8}{3}\)

b) Tìm x nguyên để A nguyên

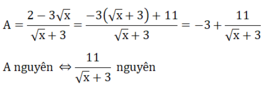
⇔ x  + 3 ∈ Ư(11) ⇔ x + 3 ∈ {-11; -1; 1; 11}

Do  x  + 3 ≥ 3 nên  x  + 3 = 11 ⇔  x  = 8 ⇔ x = 64

Vậy với x = 64 thì A nguyên