lời giải đáp án chi tiết

Những câu hỏi liên quan
Lời giải đáp án chi tiết nhé
Đọc tiếp
Lời giải đáp án chi tiết nhé
Cho em lời giải chi tiết và đáp án nhanh ạ

\(\left(a-b\right)^2=a^2-2ab+b^2=144\\ \Leftrightarrow154-2ab=144\\ \Leftrightarrow ab=5\\ \Leftrightarrow M=\left(a-b\right)^3+3ab\left(a-b\right)=12^3+3\cdot5\cdot12=1908\)
Đúng 1
Bình luận (0)
Giải cho em bài 24, có đáp án và lời giải chi tiết nha
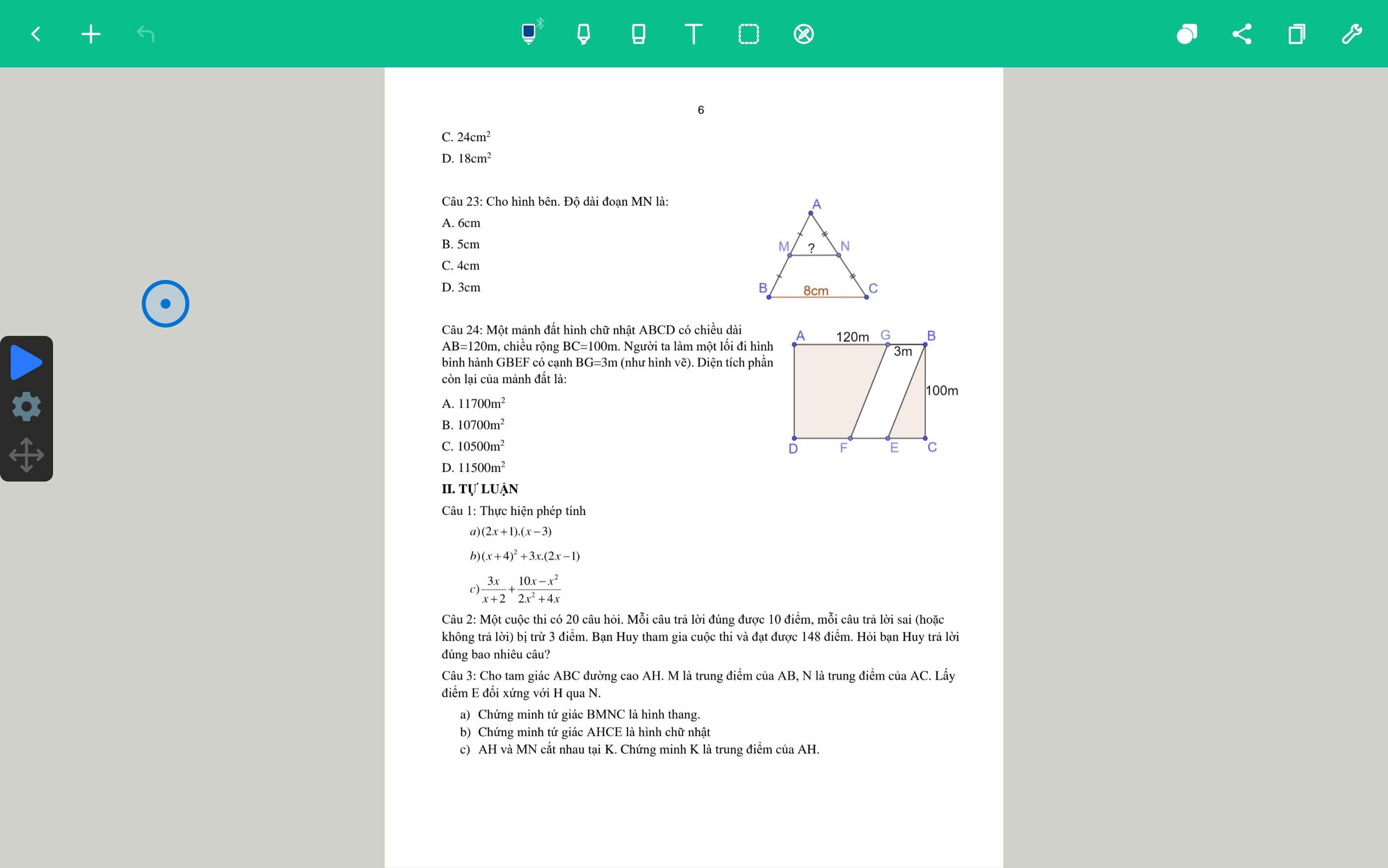
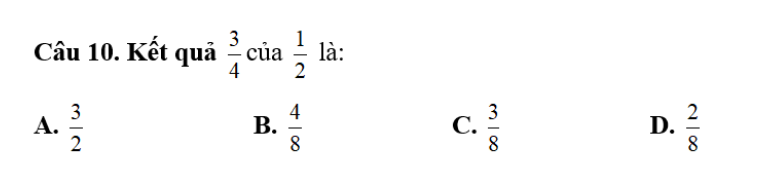
e cần xem cần lời giải chi tiết kèm đáp án ạ
Xem thêm câu trả lời
Ai giúp mình với, mình cần đáp án và lời giải chi tiết ạ!


Câu 1: C
Câu 6: B
Câu 7: A
Câu 12: B
Đúng 0
Bình luận (0)
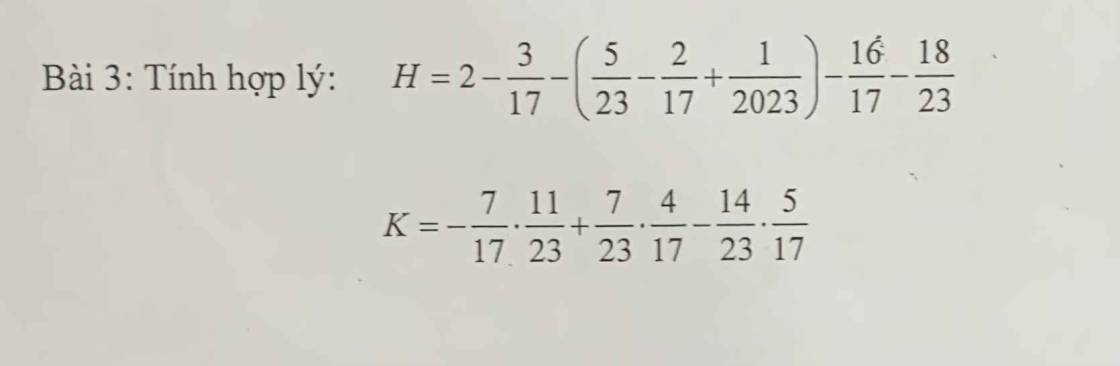 Giúp em cả đáp án và lời giải chi tiết vs ạ, em cảm ơn
Giúp em cả đáp án và lời giải chi tiết vs ạ, em cảm ơn
Lời giải:
\(H=2-\frac{3}{17}-\frac{5}{23}+\frac{2}{17}-\frac{1}{2023}-\frac{16}{17}-\frac{18}{23}\\ =2-(\frac{3}{17}-\frac{2}{17}+\frac{16}{17})-(\frac{5}{23}+\frac{18}{23})-\frac{1}{2023}\\ =2-1-1-\frac{1}{2023}=-\frac{1}{2023}\)
---------------------
\(K=\frac{7}{23}.\frac{-11}{17}+\frac{7}{23}.\frac{4}{17}-\frac{7}{23}.\frac{10}{17}\\ =\frac{7}{23}(\frac{-11}{17}+\frac{4}{17}-\frac{10}{17})\\ =\frac{7}{23}.\frac{-17}{17}=\frac{-7}{23}\)
Đúng 1
Bình luận (0)
m.n cho đáp án lời giải chi tiết nhé , cần gấp ạ ( x-1) (y+5)=28 ạ
tìm ba số có tích=tổng
mình biết đáp án rồi nhưng chưa biết lời giải nhớ giải chi tiết ra giùm mình nha
đáp án:1,2,3
Giải
a+b+c = abc (1)
Trường hợp 1 : a.b.c = 0 ⇒⇒ a+b+c = 0 mà a, b, c ≥0≥0 ⇒⇒ a=b=c=0 ( thỏa mãn )
Trường hợp 2 a.b.c > 0 ⇒⇒ a, b, c > 0
Vì vai trò của a, b, c bình đẳng nên có thể giả sử a≤b≤ca≤b≤c ⇒⇒ abc = a + b + c ≤≤ 3c ⇒⇒ ab ≤≤ 3 ( vì c> 0 )
Mà a≤ba≤b nên a2≤ab≤3a2≤ab≤3 ⇒⇒ a = 1
Thay a = 1 vào (1) ta có b+c+1 = bc ⇔⇔ (b-1) (c-1) = 2
Mà 0≤b−1≤c−10≤b−1≤c−1 nên b-1 = 1, c-1 =2 ⇒⇒ b=2, c= 3
Thử lại thấy đúng ⇒⇒ (a, b, c) = (0, 0, 0) , (1, 2 , 3) , (1, 3, 2), ( 2, 1, 3) , ( 2, 3, 1 ) , ( 3, 1, 2 ) , ( 3, 2, 1 )
Bạn tham khảo nhé
Đúng 0
Bình luận (0)
E biết đáp án rồi nma vẫn hơi mơ hồ nên mn cho em lời giải chi tiết xíu zới ạ :3

\(\Leftrightarrow\left(x^2-x\right)^2-x^2+x-30=0\)
\(\Leftrightarrow\left(x^2-x\right)^2-\left(x^2-x\right)-30=0\)
\(\Leftrightarrow\left(x^2-x-6\right)\left(x^2-x+5\right)=0\)
\(\Leftrightarrow x^2-x-6=0\)
=>(x-3)(x+2)=0
=>x=3 hoặc x=-2
Đúng 7
Bình luận (0)
`(x^2 -x)^2 +x=x^2 +30`
`<=>(x^2 -x)^2 -(x^2 -x)-30=0`
Đặt `t=x^2 -x`
`t^2 -t-30=0`
`<=>t^2 -6t+5t-30=0`
`<=>t(t-6)+5(t-6)=0`
`<=>(t-6)(t+5)=0`
`<=>[(t-6=0),(t+5=0):}`
`<=>[(x^2 -x-6=0),(x^2 -x+5=0):}`
`<=>x^2 -x-6=0`
`<=>x^2 -3x+2x-6=0`
`<=>x(x-3)+2(x-3)=0`
`<=>(x-3)(x+2)=0`
`<=>[(x-3=0),(x+2=0):}`
`<=>[(x=3),(x=-2):}`
Vậy `S={-2;3}`
Đúng 6
Bình luận (0)
`(x^2-x)^2+x=x^2+30`
`<=>(x^2-x)^2-(x^2-x)-30=0`
Đặt `x^2-x=t` khi đó ptr có dạng:
`t^2-t-30=0`
`<=>t^2-6t+5t-30=0`
`<=>(t-6)(t+5)=0`
`<=>t=6` hoặc `t=-5`
`@t=6<=>x^2-x=6`
`<=>x^2-x-6=0`
`<=>x^2-3x+2x-6=0`
`<=>(x-3)(x+2)=0<=>x=3` hoặc `x=-2`
`@t=-5<=>x^2-x=-5`
`<=>x^2-x+5=0`
Ptr có:`\Delta=(-1)^4-4.5=-19 < 0`
`=>` Ptr vô nghiệm
Vậy `S={-2;3}`
Đúng 6
Bình luận (0)

























