Xem lại đề đi em, thiếu điều kiện nên không giải được!

a, Xét tam giác MDE và tam giác MPQ có 

^M _ chung ; \(\frac{MD}{MP}=\frac{ME}{MQ}=\frac{1}{2}\)

Vậy tam giác MDE ~ tam giác MPQ (c.g.c) 

\(\frac{MD}{MP}=\frac{DE}{PQ}\Rightarrow DE=\frac{MD.PQ}{MP}=10cm\)

Bài 2:

b: Xét ΔABC có 

M là trung điểm của AC

N là trung điểm của AB

Do đó: MN là đường trung bình của ΔABC

Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(1\right)\)

Xét ΔGBC có 

K là trung điểm của GB

I là trung điểm của GC

Do đó: KI là đường trung bình của ΔGBC

Suy ra: KI//BC và \(KI=\dfrac{BC}{2}\left(2\right)\)

Từ (1) và (2) suy ra NM//KI và NM=KI

Xét tứ giác NMIK có 

NM//KI

NM=KI

Do đó: NMIK là hình bình hành

a)  xét tam giác MQK vg tại M và tam giác TQK vg tại T có 

QK chung

Góc MQK = góc TQK (gt)

=> tam giác MQK = tam giác TQK ( ch.gn)

b) xét tam giác NQK và tam giác PQK có

QK chung 

Góc NQK = góc PQK (gt)

QN = QP (gt)

=> tam giác NQK = tam giác PQK (c.g.c)

=> NK = PK

  Bạn xem lại đề đi nhé;-; lỗi quá nhiều.

Sửa đề:

Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:

a) Tứ giác MQFE là hình bình hành

b) Trung điểm của MF thuộc đường thẳng QE

GIẢI 

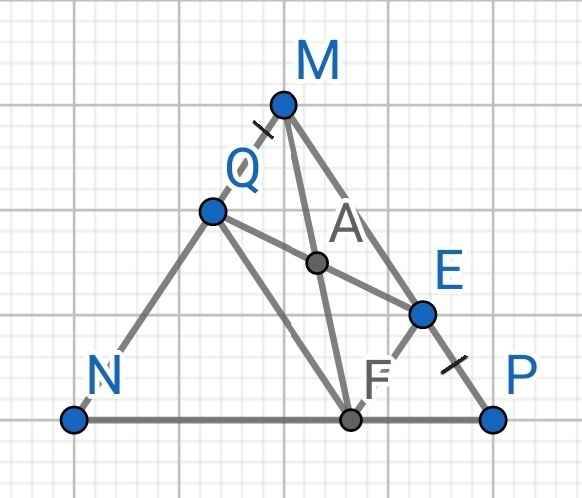
a) Do ∆MNP cân tại M (gt)

⇒ MN = MP

Mà MQ = PE (gt)

⇒ MN - MQ = MP - ME

⇒ QN = ME

Do QF // MP (gt)

⇒ ∠QFN = ∠MPN (đồng vị) (1)

Mà ∆MNP cân tại M

⇒ ∠MPN = ∠MNP

⇒ ∠MPN = ∠QNF (2)

Từ (1) và (2) ⇒ ∠QFN = ∠QNF

⇒ ∆QNF cân tại Q

⇒ QN = QF

Mà QN = ME (cmt)

⇒ QF = ME

Do QF // MP (gt)

⇒ QF // ME

Tứ giác MQFE có:

QF // ME (cmt)

QF = ME (cmt)

⇒ MQFE là hình bình hành

b) Gọi A là trung điểm của MF

Do MQFE là hình bình hành

⇒ A là trung điểm của hai đường chéo MF và QE

⇒ A là trung điểm của QE

⇒ A ∈ QE