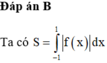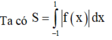. f) [x] = 0,35 và x > 0.

Những câu hỏi liên quan
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(-1)0f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x),y0,x-1 và x1. Mệnh đề nào sau đây đúng? A.
S
∫
-
1
0
f
(
x
)
d
x
+
∫
0
1
|
f
(
x
)
|
d
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(-1)>0<f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x),y=0,x=-1 và x=1. Mệnh đề nào sau đây đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 | f ( x ) | d x
B. S = ∫ - 1 1 | f ( x ) | d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
Cho các đa thức f(x),�(�), g(x)�(�) và h(x).ℎ(�). Xét các tập hợp X{x∈R|f(x)0},�{�∈�|�(�)0}, Y{x∈R|g(x)0},�{�∈�|�(�)0}, Z{x∈R|h(x)0}�{�∈�|ℎ(�)0} và T{x∈R|f2(x)+|g(x)|+√h(x)≤0}.�{�∈�|�2(�)+|�(�)|+ℎ(�)≤0}. Trong các mệnh đề dưới đây, mệnh đề nào đúng ?A. TX∪Y∪Z.��∪�∪�.B. TX∩Y∩Z.��∩�∩�.C. TX
Đọc tiếp
Cho các đa thức và Xét các tập hợp và Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A.
B.
C.
Cho hàm số y f(x) liên tục trên R và thỏa mãn f(-1)0f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x); y0; x-1 và x1Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1)>0<f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x); y=0; x=-1 và x=1Mệnh đề nào sau đây đúng?
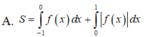
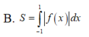
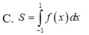
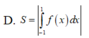
Cho hai đa thức f (x)3x3 +5x−2x2 −7 và g(x)3x3 −(2x2 −5x)+7x2 +3 a/ Thu gọn và sắp xếp f(x), g(x) theo thứ tự bậc giảm dần. Tìm bậc của chúng b/Tính N(x)g(x)−f(x) và M(x)2.f(x)+g(x) c/ Tính giá trị của M(x) biết x2-3x0 d/ Tìm giá trị nhỏ nhất của N(x).
Đọc tiếp
Cho hai đa thức f (x)=3x3 +5x−2x2 −7 và g(x)=3x3 −(2x2 −5x)+7x2 +3
a/ Thu gọn và sắp xếp f(x), g(x) theo thứ tự bậc giảm dần. Tìm bậc của chúng b/Tính N(x)=g(x)−f(x) và M(x)=2.f(x)+g(x)
c/ Tính giá trị của M(x) biết x2-3x=0 d/ Tìm giá trị nhỏ nhất của N(x).
a: F(x)=3x^3-2x^2+5x-7
G(x)=3x^3-2x^2+5x+7x^2+3=3x^3+5x^2+5x+3
Bậc của F(x),G(x) đều là 3
b: N(x)=G(x)-F(x)
\(=3x^3+5x^2+5x+3-3x^3+2x^2-5x+7=7x^2+10\)
M(x)=2F(x)+G(x)
\(=6x^3-4x^2+10x-14+3x^3+5x^2+5x+3\)
\(=9x^3+x^2+15x-11\)
c: x^2-3x=0
=>x=0 hoặc x=3
\(M\left(0\right)=9\cdot0^3+0^2+15\cdot0-11=-11\)
\(M\left(3\right)=9\cdot3^3+3^2+15\cdot3-11=286\)
d: N(x)=7x^2+10>=10
Dấu = xảy ra khi x=0
Đúng 1
Bình luận (0)
Bài 7 : Tìm x thuộc Q , biết :
a. | x | = 3/4 và x < 0
b. | x | = 0,35 và x > 0
c. | x | = 2,1
d. | x | = -1 và 2/5
e. | x-1 | + | x-4 | = 3x
f. | x+1 | + | x+4 | = 3x
g. | x( x-4 ) | = x
Bài 7 : Tìm x thuộc Q , biết :
a. | x | = 3/4 và x < 0
b. | x | = 0,35 và x > 0
c. | x | = 2,1
d. | x | = -1 và 2/5
e. | x-1 | + | x-4 | = 3x
f. | x+1 | + | x+4 | = 3x
g. | x( x-4 ) | = x
Tìm x ∈ Q, biết: |x| = 0,35 và x > 0
Bài 1 : Cho \(f\left(x\right)=x^3-2ax+b\). Tìm a,b biết đa thức có hai nghiệm là f(1)=-1 và f(0)=2
Bài 2 . Cho \(f\left(x\right)=x^3-2ax+b\). TÌm a,b biết đa thức có hai nghiệm là 0 và 3
Cho đa thức f(x) thoả mãn: x.f(x + 1) = (x + 2).f(x).
CTR đa thức f(x) có ít nhất 2 nghiệm là 0 và -1
Nếu x = 0
=> 0. f(1) = 2. f(0)
=> 0 = 2 . f(0)
=> f(0) = 0
=> x = 0
=> x = 0 là 1 nghiệm của đa thức f(x) ( 1 )
Nếu x = - 2
=> ( -2 ). f(- 1) = 0. f(- 2)
=> (-2 ). f(- 1 ) = 0
=> f(- 1) = 0
=> x = -1
=> x = -1 là 1 nghiệm của đa thức f(x) ( 2 )
Từ ( 1 ) và ( 2 ) => Đa thức f(x) có ít nhất 2 nghiệm là 0 và - 1
Đúng 0
Bình luận (0)