Làm phếp tính cộng các phân thức sau 2x-3y/xy-y²+1/x-y

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử:
1, 2(x-1)3-(x-1)
2, y(x-2y)2+xy2(2y-x)
3, xy(x+y)-2x-y
4, xy(x-3y)-2x+6y
1) \(2\left(x-1\right)^3-\left(x-1\right)=\left(x-1\right)\left(2\left(x-1\right)^2-1\right)\)
2) \(y\left(x-2y\right)^2+xy^2\left(2y-x\right)=\left(2y-x\right)\left(2\left(2y-x\right)+1\right)=\left(2y-x\right)\left(4y-2x+1\right)\)
3) \(xy\left(x+y\right)-x-y=xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\) (xem lại đề sửa -2x thành -x mới đúng)
4) \(xy\left(x-3y\right)-2x+6y=xy\left(x-3y\right)-2\left(x-3y\right)=\left(x-3y\right)\left(xy-2\right)\)
Đúng 1
Bình luận (0)
*Cộng các phân thức sau: a) x^2/x+1 + 2x/x^2-1 + 1/1+x+1 b) 2x+y/2x^2-y + 8y/y^2-4x^2+2x-y/2x^2+xy c) 1/x-y +3xy/y^3-x^3 + x-y/x^2+xy+y^2
*Cộng các phân thức sau:
a) x^2/x+1 + 2x/x^2-1 + 1/1+x+1
b) 2x+y/2x^2-y + 8y/y^2-4x^2+2x-y/2x^2+xy
c) 1/x-y +3xy/y^3-x^3 + x-y/x^2+xy+y^2
plz
Xem chi tiết
a, \(\frac{x^2}{x+1}+\frac{2x}{x^2-1}+\frac{1}{x+1}+1\)
\(=\frac{x^2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\frac{2x}{\left(x-1\right)\left(x+1\right)}+\frac{x-1}{\left(x+1\right)\left(x-1\right)}+\frac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^3-x^2-2x+x-1-x^2-1}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x^3-2x^2-x-2}{\left(x-1\right)\left(x+1\right)}\)
Bài 1 Phân tich các đa thức sau thành nhân tử: a) x(2x -y) - y(2x -y) c) x^2- 3x + 3y -y^2 b) x²–6x - 7 d) x³- xy + 2y - 8
a: \(x\left(2x-y\right)-y\left(2x-y\right)=\left(2x-y\right)\left(x-y\right)\)
c: \(x^2-3x+3y-y^2\)
\(=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-3\right)\)
b: \(x^2-6x-7=\left(x-7\right)\left(x+1\right)\)
Đúng 2
Bình luận (0)
a) \(x\left(2x-y\right)-y\left(2x-y\right)=\left(2x-y\right)\left(x-y\right)\)
b) \(x^2-6x-7=x\left(x-7\right)+\left(x-7\right)=\left(x-7\right)\left(x+1\right)\)
c) \(x^2-3x+3y-y^2=\left(x-y\right)\left(x+y\right)-3\left(x-y\right)=\left(x-y\right)\left(x+y-3\right)\)
d) \(x^3-xy+2y-8=\left(x-2\right)\left(x^2+2x+4\right)-y\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+2x+4-y\right)\)
Đúng 1
Bình luận (0)
a)x(2x - y) - y(2x - y)
= (x - y)(2x - y)
c)x2 - 3x + 3y - y2
= x2 - y2 - 3x + 3y
= (x + y)(x - y) - 3(x - y)
= (x + y - 3)(x - y)
b)x2 - 6x - 7
= x2 + x - 7x - 7
= x(x + 1) - 7(x + 1)
= (x - 7)(x + 1)
d)x3 - xy + 2y - 8
= x3 - 8 - xy + 2y
= x3 - 23 - y(x - 2)
= (x - 2)(x2 + 2x + 4) - y (x - 2)
= (x - 2 - y)(x2 + 2x + 4)
Đúng 1
Bình luận (0)
Bài 1: Phân tích đa thức sau :
a)2x(xy+y^2-3)
b)(x-y)(2x+y)
c)(x-2y)^2
d)(2x-y)(y+2x)
bài 2: Phân tích các đơn thức thành nhân tử
a)3x^2-3xy
b)x^2-4y^2
c)3x-3y+xy-y^2
d)x^2-1+2y-y^2
Bài 3: Tìm x biết:
a)3x^2-6x=0
b)Tìm x,y thuộc z biết: x^2+4y^2-2xy=4
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
Đúng 2
Bình luận (0)
Cho các số 5x - y; 2x + 3y; x + 2y lập thành cấp số cộng ; các số (y + 1)2, xy + 1, (x – 1)2 lập thành cấp số nhân. Tính x; y.
Đọc tiếp
Cho các số 5x - y; 2x + 3y; x + 2y lập thành cấp số cộng ; các số (y + 1)2, xy + 1, (x – 1)2 lập thành cấp số nhân. Tính x; y.
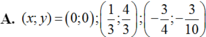
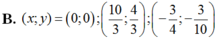
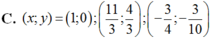
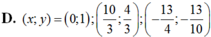
Chọn B.
+ Ta có các số 5x - y; 2x + 3y; x + 2y lập thành CSC nên suy ra
2( 2x + 3y) = 5x – y + x+ 2y hay 2x = 5y (1)
Các số (y + 1)2, xy + 1, (x – 1)2 lập thành CSN suy ra (xy + 1)2 = (y + 1)2(x – 1)2 ⇔ (4 + 2y – 2x)(4xy + 2x – 2y) = 0 (2)
Thay (1) vào (2) ta được: (4 + 2y – 5y)(10y2 + 5y – 2y) = 0
⇔ y(4 – 3y)(10y + 3) = 0 ⇔ y = 0, y = 4/3, y = -3/10.
Vậy 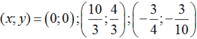
Đúng 0
Bình luận (0)
*Cộng các phân thức sau:a) x^2/x+1 + 2x/x^2-1 + 1/1+x+1 b) 2x+y/2x^2-y + 8y/y^2-4x^2+2x-y/2x^2+xy
a) \(\dfrac{x^2}{x+1}+\dfrac{2x}{x^2-1}+\dfrac{1}{1+x+1}\) \(=\dfrac{x^2.\left(x-1\right)\left(x+2\right)}{\left(x+1\right).\left(x-1\right)\left(x+2\right)}+\dfrac{2x.\left(x+2\right)}{\left(x-1\right).\left(x+1\right).\left(x+2\right)}+\dfrac{\left(x-1\right).\left(x+1\right)}{\left(x-1\right)\left(x+1\right).\left(x+2\right)}\)
\(=\dfrac{x^2.\left(x-1\right).\left(x+2\right)+2x.\left(x+2\right)+\left(x-1\right)\left(x+1\right)}{\left(x+1\right).\left(x-1\right).\left(x+2\right)}\)
\(=\dfrac{x^4+x^3-2x^2+2x^2+4x+x^2-1}{\left(x-1\right)\left(x+1\right).\left(x+2\right)}\)
\(=\dfrac{x^4+x^3+x^2+4x-1}{\left(x^2-1\right).\left(x+2\right)}\)
\(=\dfrac{x^4+x^3+x^2+4x-1}{x^3+2x^2-x-2}\)
Đúng 0
Bình luận (0)
Cộng các phân thức:
a) x/xy-y^2 + 2x-y/xy-x^2
b) 1/x+1 + 1/x-1 + 2x^2/x^2-1
a, \(\frac{x}{xy-y^2}+\frac{2x-y}{xy-x^2}=\frac{x}{y\left(x-y\right)}+\frac{2x-y}{x\left(y-x\right)}\)
\(=\frac{x^2}{xy\left(x-y\right)}-\frac{2xy-y^2}{xy\left(x-y\right)}=\frac{\left(x-y\right)^2}{xy\left(x-y\right)}=\frac{x-y}{xy}\)
b, \(\frac{1}{x+1}+\frac{1}{x-1}+\frac{2x^2}{x^2-1}=\frac{x-1}{\left(x+1\right)\left(x-1\right)}+\frac{x+1}{\left(x-1\right)\left(x+1\right)}+\frac{2x^2}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x-1+x+1+2x^2}{\left(x-1\right)\left(x+1\right)}=\frac{2x+2x^2}{\left(x-1\right)\left(x+1\right)}=\frac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{2x}{x-1}\)
Cho tỉ lệ thức \(\dfrac{x}{y}=\dfrac{2}{3}\). Tính giá trị của các biểu thức sau:
\(A=\dfrac{x+5y}{3x-2y}-\dfrac{2x-3y}{4x+5y}\)
\(B=\dfrac{2x^2-xy+3y^2}{3x^2+2xy+y^2}\)
Lời giải:
$\frac{x}{y}=\frac{2}{3}\Rightarrow \frac{x}{2}=\frac{y}{3}$. Đặt $\frac{x}{2}=\frac{y}{3}=k$ thì:
$x=2k; y=3k$
Khi đó: $3x-2y=3.2k-3.2k=0$. Mẫu số không thể bằng $0$ nên $A$ không xác định. Bạn xem lại.
$B=\frac{2(2k)^2-2k.3k+3(3k)^2}{3(2k)^2+2.2k.3k+(3k)^2}=\frac{29k^2}{33k^2}=\frac{29}{33}$
Đúng 2
Bình luận (0)























