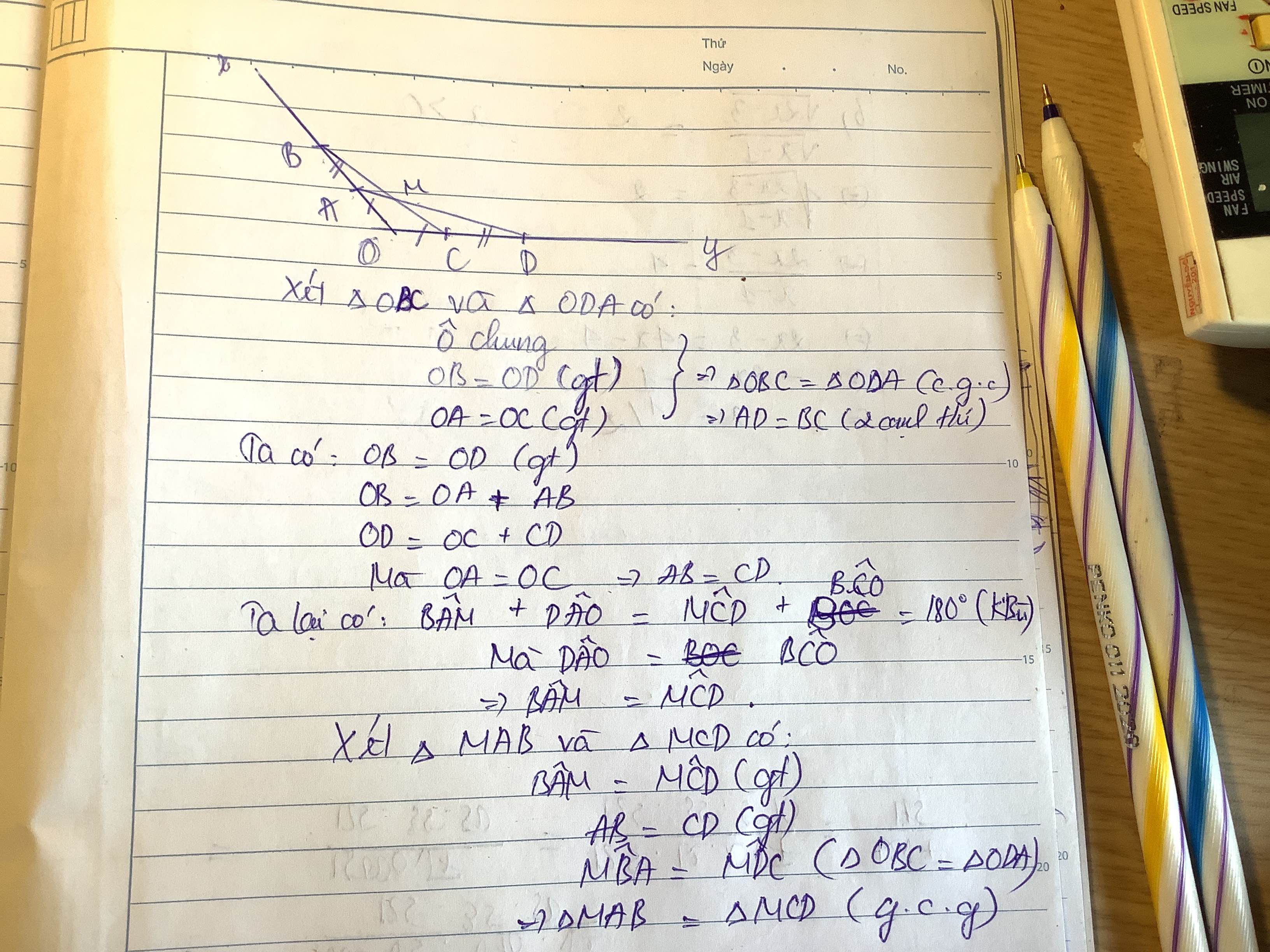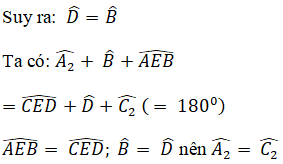Bài 1: Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA

Những câu hỏi liên quan
Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA
Xem chi tiết
Bài 1: Cho góc xOy khác góc bẹt lấy các điểm A, B thuộc tia Ox sao cho OA < OB.
Lấy điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB.
Gọi E là giao điểm của AD và BC. Chứng minh:
a) AD = BC b) DEAB = DECD c) OE là phân giác của góc xOy
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB
Đúng 0
Bình luận (0)
Bài 1: Cho góc xOy khác góc bẹt, trên tia Ox lấy các điểm A, B sao cho OA < OB. Lấy điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh: a) AD = BC. b) EAB = ECD. c) OE là phân giác của góc xOy. d) AC// BD.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
OE là tia phân giác của góc xOy
ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc xoy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho OA< OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC chứng minh rằng. A) AD= BC B) ∆EAB= ∆ECD C)OE là tia phân giác của góc xOy. Giải giúp e câu C với ạ.
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
Đúng 1
Bình luận (0)
Bài 8:Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OB = OD. Gọi M là giao điểm của AD và BC. Chứng minh rằng: a) AD = BC. b)tam giác MAB = tam giác MCD
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{MAB}=180^0-\widehat{OAD}\)
và \(\widehat{MCD}=180^0-\widehat{OCB}\)
nên \(\widehat{MAB}=\widehat{MCD}\)
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD
Đúng 1
Bình luận (0)
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
a) AD = BC
b) ΔEAB = ΔECD
c) OE là tia phân giác của góc xOy
a)
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
Đúng 1
Bình luận (0)
c) Ta có:
ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: BOE=DOE
hay OE là tia phân giác của góc xOy
Đúng 1
Bình luận (0)
Bài 43 (trang 125 SGK Toán 7 Tập 1): Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA OB. Lấy các điểm C, D thuộc tia Oy sao cho OC OA, OD OB. Gọi E là giao điểm của AD và BC. Chứng minh rằnga) AD BCb) ΔEAB ΔECDc) OE là tia phân giác của góc xOyBài 44 (trang 125 SGK Toán 7 Tập 1): Cho ΔABC có góc B góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằnga) ΔADB ΔADCb) AB ACVẽ hìnhHELP ME !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Đọc tiếp
Bài 43 (trang 125 SGK Toán 7 Tập 1): Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
a) AD = BC
b) ΔEAB = ΔECD
c) OE là tia phân giác của góc xOy
Bài 44 (trang 125 SGK Toán 7 Tập 1): Cho ΔABC có góc B = góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng
a) ΔADB = ΔADC
b) AB = AC
Vẽ hình
HELP ME !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
![]()
Bài 44:
a: Xét ΔADB và ΔADC có
\(\widehat{ADB}=\widehat{ADC}\)
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
Do đó:ΔADB=ΔADC
b: Xét ΔABC có \(\widehat{B}=\widehat{C}\)
nên ΔABC cân tại A
Đúng 0
Bình luận (0)
Bài 43 (trang 125 SGK Toán 7 Tập 1): Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA OB. Lấy các điểm C, D thuộc tia Oy sao cho OC OA, OD OB. Gọi E là giao điểm của AD và BC. Chứng minh rằnga) AD BCb) ΔEAB ΔECDc) OE là tia phân giác của góc xOyBài 44 (trang 125 SGK Toán 7 Tập 1): Cho ΔABC có góc B góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằnga) ΔADB ΔADCb) AB ACCó vẽ hìnhHELP ME !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!(Đăng lại vì ko ai giúp ;-; )
Đọc tiếp
Bài 43 (trang 125 SGK Toán 7 Tập 1): Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng
a) AD = BC
b) ΔEAB = ΔECD
c) OE là tia phân giác của góc xOy
Bài 44 (trang 125 SGK Toán 7 Tập 1): Cho ΔABC có góc B = góc C. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng
a) ΔADB = ΔADC
b) AB = AC
Có vẽ hình
HELP ME !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
(Đăng lại vì ko ai giúp ;-; )
Bài 43
a) ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
b) Do ΔOAD = ΔOCB (chứng minh trên)
OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔAEB và ΔCED có:
∠B = ∠D
AB = CD
∠A2 = ∠C2
⇒ΔAEB = ΔCED (g.c.g)
c) ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒ 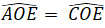
Bài 44
a)
Do đó ΔADB = ΔADC (g.c.g)
b) ΔADB = ΔADC ( câu a )
Suy ra AB = AC (hai cạnh tương ứng)
Đúng 1
Bình luận (1)