\(f\left(x\right)=2x+\dfrac{3}{2x-4}-\left(3+\dfrac{3}{2x-4}\right)\)

\(f\left(x\right)=2x+\dfrac{3}{2x-4}-3-\dfrac{3}{2x-4}\)

\(f\left(x\right)=2x-3\)

Để f(x) âm thì :

\(2x-3< 0\)

\(\Leftrightarrow2x< 3\)

\(\Leftrightarrow x< \dfrac{3}{2}\)

Vậy C đúng

Have a nice day!

Chọn C

Ta có 

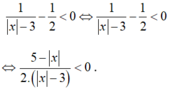
Đặt  bpt trở thành 

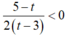
Bảng xét dấu

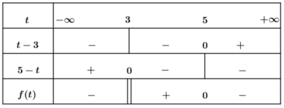
Căn cứ bảng xét dấu ta được 

Chọn D.

Để f(x) = x(5x + 2) - x( x 2  + 6) không dương thì

x(5x + 2) - x(x2 + 6) ≤ 0 ⇔ x( x 2  - 5x + 4) ≥ 0

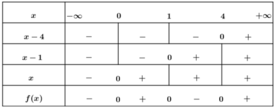
Vậy x ∈ [0;1] ∪ [4; + ∞ ).

\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)

\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)

=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)

C=-1 ta được phương án A(ko tm câu hỏi)

C=0 ta được phương án B(ko tm câu hỏi)

C=2 ta được phương án C(ko tm câu hỏi)

=>chọn D

a) Để \(\sqrt{\dfrac{x}{3}}\) có nghĩa thì \(\dfrac{x}{3}\ge0\Leftrightarrow x\ge0\)

b) Để \(\sqrt{-5x}\) có nghĩa thì \(-5x\ge0\Leftrightarrow x\le0\)

c) Để \(\sqrt{4-x}\) có nghĩa thì \(4-x\ge0\Leftrightarrow x\le4\)

d) Để \(\sqrt{3x+7}\) có nghĩa thì \(3x+7\ge0\Leftrightarrow x\ge-\dfrac{7}{3}\)

e) Để \(\sqrt{-3x+4}\) có nghĩa thì \(-3x+4\ge0\Leftrightarrow x\le\dfrac{4}{3}\)

f) Để \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa thì \(\left\{{}\begin{matrix}\dfrac{1}{-1+x}\ge0\\-1+x\ne0\end{matrix}\right.\)

\(\Leftrightarrow-1+x>0\Leftrightarrow x>1\)

g) Để \(\sqrt{1+x^2}\) có nghĩa thì \(1+x^2\ge0\left(đúng\forall x\right)\)

h) \(\sqrt{\dfrac{5}{x-2}}\) có nghĩ thì \(\left\{{}\begin{matrix}\dfrac{5}{x-2}\ge0\\x-2\ne0\end{matrix}\right.\)

\(\Leftrightarrow x-2>0\Leftrightarrow x>2\)

a. \(x\ge0\)

b. \(x< 0\)

c. \(x\le4\)

d. \(x\ge\dfrac{-7}{3}\)

e. \(x\le\dfrac{4}{3}\)

f. \(x>1\)

g. Mọi x

h. \(x>2\)

Xét f(x) = \(x\left(x^2-1\right)=x\left(x-1\right)\left(x+1\right)\)

f(x) = 0 khi x = 0 hoặc x = 1 hoặc x = -1

Ta có bảng

x            \(-\infty\)             -1              0               1                  \(+\infty\)  

x                        -        |        -      0       +       |        +  

x-1                     -        |        -       |       -        0       +

x+1                    -        0       +      |       +        |        +

f(x)                     -        0       +     0       -        0       +

=> f(x) \(\ge0\Leftrightarrow x\in\left[-1;0\right]\cup\left[1;+\infty\right]\)

Chọn A

Chọn B

B

Ko bt :)

2: ĐKXĐ: x<>1

\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)

\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)

\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)

f'(x)=0

=>x^2-2x=0

=>x(x-2)=0

=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

1:

\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)

=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)

f'(x)=0

=>\(\left(x-2\sqrt{2}\right)^2=0\)

=>\(x-2\sqrt{2}=0\)

=>\(x=2\sqrt{2}\)