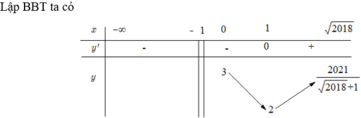
Cho hàm số y = x 2 + m ( 2018 - x 2 + 1 ) - 2021 với m là tham số thực. Gọi S là tổng tất cả các giá trị nguyên của tham số m để đồ thị của hàm số đã cho cắt trục hoành tại đúng hai điểm phân biệt. Tính S.
A. 960
B. 986
C. 984
D. 990




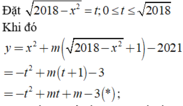


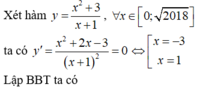
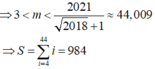
















 , cây này chỉ tạo một loại giao tử mang hai gen lặn ab => kiểu hình ở con lai F1 do giao tử của cây P dị hợp quyết định.
, cây này chỉ tạo một loại giao tử mang hai gen lặn ab => kiểu hình ở con lai F1 do giao tử của cây P dị hợp quyết định. AB/ab (lá dài, quăn) x ab/ab (lá ngắn, thẳng)
AB/ab (lá dài, quăn) x ab/ab (lá ngắn, thẳng)

