giúp tôi giải câu này với

Chọn C

a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:

- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5

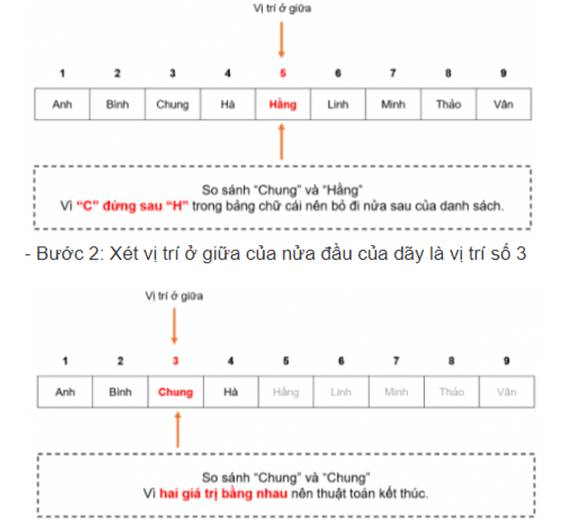
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.

b) Thuật toán tìm kiếm nhị phân

- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.

Thuật toán tuần tự

- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.

- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.

- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.

Trong trường hợp này, chúng ta cần tìm phần tử có giá trị là 47 trong dãy A = [1, 91, 45, 23, 67, 9, 10, 47, 90, 46, 86]. Ta sẽ thực hiện duyệt từng phần tử trong dãy này để tìm kiếm phần tử có giá trị là 47.

Dãy A có tổng cộng 11 phần tử, và trong trường hợp xấu nhất, phần tử cần tìm là phần tử cuối cùng của dãy. Vì vậy, trong trường hợp xấu nhất, ta cần duyệt qua toàn bộ dãy A để tìm thấy phần tử có giá trị là 47.

Vậy, số lần duyệt cần thực hiện là 7 lần.

Ước lượng số phép toán sơ cấp cần thực hiện

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    ll a[]={10,2,5,12,20,6,8,15,18}; //mảng đã cho
    ll n=sizeof(a)/sizeof(a[0]); //độ dài mảng
    sort(a,a+n); //sắp xếp mảng
    //Thuật toán tìm kiếm nhị phân
    ll l=0, r=n-1;
    while(l<=r) {
        ll mid=(l+r)/2; //Tìm phần tử giữa left và right
        if(a[mid]<15) l=mid+1; //Vì từ đoạn [0,mid] thì phần tử nhỏ hơn 15 nên ta duyệt từ khoảng (mid,r]
        else r=mid-1; //vì thấy nên rút r để thu hẹp phạm vi
    }
    cout << l+1; //in ra kq (vì bắt đầu từ 0 đến n-1 nên phải tăng thêm để ra vị trí đúng)
}

(Bạn có thể dựa vào code mình để rút ra các bước)

Chúc bạn học tốt!

#include <bits/stdc++.h>

using namespace std;

long long i,n,x,k;

int main()

{

cin>>n>>k;

for (i=1; i<=n; i++)

{

cin>>x;

if (x==k) cout<<i<<" ";

}

return 0;

}