A=(4a2-3a+17)/(a3-1)+(2a-1)/(a2+a+1)+(6)/(1-a) a/ Tìm điều kiện của A để biểu thức A được xác định. b/ Rút gọn A c/ Tìm a nguyên để A nhận giá trị nguyên âm

Những câu hỏi liên quan
Cho phân thức
A= \(\dfrac{x^2-6x+9}{x^2-x-6}\)
a, Tìm điều kiện của x để giá trị của A được xác định
b, Rút gọn A
c, Tìm x∈Z để giá trị của A nguyên
\(a,ĐK:x\ne3;x\ne-2\\ b,A=\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x+2\right)}=\dfrac{x-3}{x+2}\\ c,A\in Z\Leftrightarrow\dfrac{x+2-5}{x+2}=1-\dfrac{5}{x+2}\in Z\\ \Leftrightarrow x+2\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow x\in\left\{-7;-3;-1;3\right\}\left(tm\right)\)
Đúng 1
Bình luận (0)
cho biểu thức C=\(\dfrac{x^3}{x^2-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}\)
a, Tìm giá trị của x để giá trị của biểu thức C được xác định
b, Tìm x để C=0
c, Tìm giá trị nguyên của x để C nhận giá trị dương
a) C được xác định <=> x khác +- 2
b) Ta có : \(C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-1\right)\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=x-1\)
Để C = 0 thì x - 1 = 0 <=> x = 1 (tm)
c) Để C nhận giá trị dương thì x - 1 > 0 <=> x > 1
Kết hợp với ĐK => Với x > 1 và x khác 2 thì C nhận giá trị dương
Đúng 1
Bình luận (1)
Cho A= x-9/3+√x ( lưu ý / là phân số) a) Tìm giá trị của x để biểu thức A có nghĩa b) Rút gọn A c) tính giá trị biểu thức A khi x=0;x=-1;x=16 d) Tìm x nguyên để A nguyên
\(A=\dfrac{x-9}{3+\sqrt{x}}\) (đề như này pk?)
a) Để A có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3+\sqrt{x}\ne0\left(lđ\right)\end{matrix}\right.\)\(\Rightarrow x\ge0\)
b) \(A=\dfrac{x-9}{3+\sqrt{x}}=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{3+\sqrt{x}}=\sqrt{x}-3\)
c) Với x=0 (tmđk) thay vào A ta được: \(A=\sqrt{0}-3=-3\)
Với x=-1 (ktm đk)
Với x=16 (tmđk) thay vào A ta được: \(A=\sqrt{16}-3=1\)
d) \(A\in Z\Leftrightarrow\sqrt{x}-3\in Z\Leftrightarrow\sqrt{x}\in Z\) \(\Leftrightarrow\) x là số chính phương
Đúng 1
Bình luận (5)
Cho biểu thức: B=\(\left[\dfrac{x+1}{2x-2}+\dfrac{3}{x^2-1}-\dfrac{x+3}{2x+2}\right].\dfrac{4x^2-4}{5}\)
a, Tìm điều kiện của x để giá trị của biểu thức được xác định
b, Chứng minh rằng: Khi giá trị của biểu thức được xác định thì nó không phụ thuộc vào giá trị
a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM
Đúng 0
Bình luận (0)
cho phân thức: \(\dfrac{2x^2-4x+8}{x^3+8}\)
a, Với điều kiện nào của x thì giá trị của phân thức xác định
b, Hãy rút gọn phân thức
c, Tính giá trị của phân thức tại x=2
d, Tìm giá trị của x để giá trị của phân thức được xác định
Bạn tham khảo nha! Mình không hiểu đề câu d lắm nên không làm câu d, nhưng theo mình đoán câu d có phải sẽ là tìm x để phân thức được giá trị nguyên có đúng không nhỉ?

Đúng 2
Bình luận (13)
cho phân thức: \(\dfrac{2x^2-4x+8}{x^3+8}\)
a, Với điều kiện nào của x thì giá trị của phân thức xác định
b, Hãy rút gọn phân thức
c, Tính giá trị của phân thức tại x=2
d, Tìm giá trị của x để giá trị của phân thức được xác định
a) Với điều kiện x ≠ -2 thì giá trị của phân thức xác định
b) \(\dfrac{2x^2-4x+8}{x^3+8}\)
= \(\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)
= \(\dfrac{2}{x+2}\)
c) Thay x = 2 vào phân thức, ta được :
\(\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
d) Với x ≠ -2 thì giá trị của phân thức được xác định
Đúng 2
Bình luận (0)
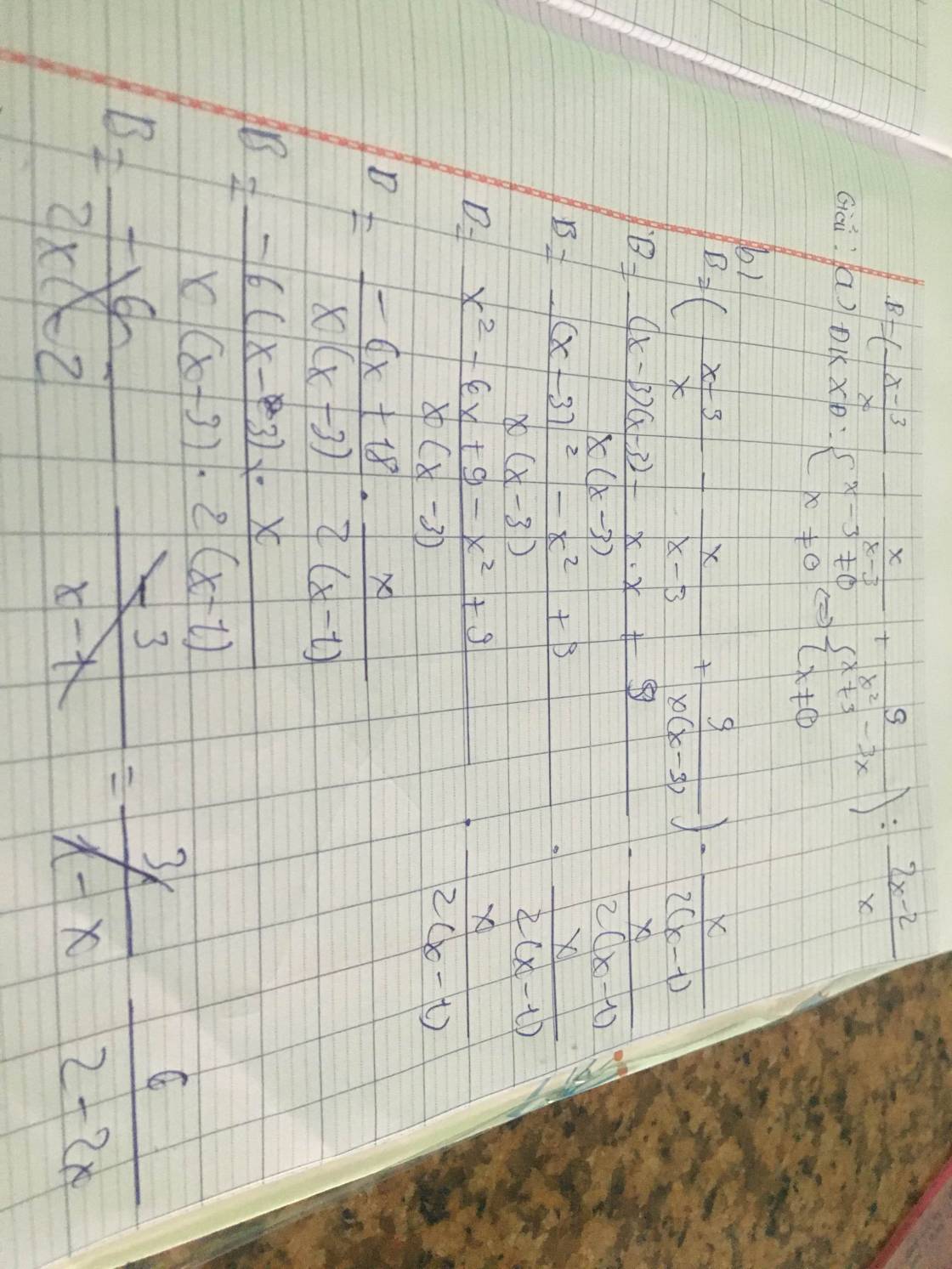
Cho biểu thức B=( x-3/ x - x / x-3 + 9/x^2-3x) :2x-2/x a, Tìm ĐKXĐ và rút gọn biểu thức B b, Tìm giá trị của x để B=2 c, Tìm giá trị nguyên của x để B nhận giá trị nguyên
Mình cần gấp ạ nhanh giúp tui :)) Cảm ơn
 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
Đúng 0
Bình luận (0)
Cho phân thức C=\(\dfrac{3x^2-x}{9x^2-6x+1}\)
a, Tính điều kiện của x để phân thức được xác định
b, Tính giá trị của phân thức tại x=-8
c, Rút gọn phân thức
`a)ĐK:9x^2-6x+1 ne 0<=>(3x-1)^2 ne 0<=>3x-1 ne 0<=>3x ne 1<=>x ne 1/3`
`b)x=-8`
`=>C=(3.64+8)/(9.64+6.8+1)`
`=8/25`
`c)C=(3x^2-x)/(9x^2-6x+1)`
`=(x(3x-1))/(3x-1)^2`
`=x/(3x-1)`
Mình thấy sai sai đáng lẽ cho rg trc rồi mới tính cho nó nhanh chứ :))
Đúng 1
Bình luận (1)
Cho biểu thức 𝐴 = 4
𝑛-1
(𝑛 ∈ 𝑍)
a) Số nguyên n phải có điều kiện gì để A là phân số?
b) Tìm tất cả các giá trị nguyên của n để A là số nguyên.
giúp mik vs
a) Ta có: \(A=\dfrac{4}{n-1}\left(n\in Z\right)\)
Để biểu thức \(A\) là phân số thì \(n-1\ne0\Leftrightarrow n\ne1\)
Vậy \(n\ne1\) thì biểu thức \(A\) là phân số.
b) Ta có: \(\dfrac{4}{n-1}\left(n\in Z\right)\)
Để biểu thức \(A\) là số nguyên thì \(n-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
\(\Rightarrow n\in\left\{2;0;3;-1;5;-3\right\}\)
Vậy \(n\in\left\{2;0;3;-1;5;-3\right\}\) thì biểu thức \(A\) là số nguyên.
Đúng 3
Bình luận (0)
a: Để A là phân số thì n-1<>0
hay n<>1
b: Để A là số nguyên thì \(n-1\inƯ\left(4\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)
Đúng 2
Bình luận (0)
a) 2-n khác 0
2n khác 4
=> n khác 2
b) 2n+1 chia hết 2n-4
2n-4+5 chia hết 2n-4
=> 2n-4+5/2n-4=2n-4/2n-4+5/2n-4=1+5/2n-4
=> 5 chia hết 2n-4
=> 2n-4 là Ư(5)=( 5;-5;1;-1)
=> 2n=(9;-1;5;3)
=> x ko thỏa mãn
Đúng 1
Bình luận (0)
Cho hai biểu thức: và với a) Tính giá trị của B biết x -1 b) Rút gọn biểu thức A c) Đặt . Tìm x Z sao cho P nhận giá trị nguyên
Đọc tiếp
Cho hai biểu thức: ![]() và
và ![]() với
với ![]()
a) Tính giá trị của B biết x = -1
b) Rút gọn biểu thức A
c) Đặt ![]() . Tìm x
. Tìm x ![]() Z sao cho P nhận giá trị nguyên
Z sao cho P nhận giá trị nguyên




























