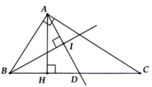
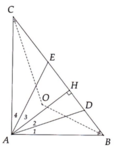
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Phân giác của góc HAC cắt nhau tại M. Chứng minh tam giác AMB vuông

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC. Phân giác của góc HAC cắt nhau tại M. Chứng minh tam giác AMB vuông
cho tam giác abc vuông tại a. kẻ ah vuông góc với bc (h thuộc bc) a) chứng minh B=HAC b)các tia phân giác của ABC vadf HAC cắt nhau tại k chứng minh tam giác AKB vuông tại k
cho tam giác abc c vuông tại a kẻ ah vuông góc bc tia phân giác của góc hac cắt bc tại d qua d kẻ dk vuông góc ac 1 chứng minh tam giác hac khd 2 chứng minh tam giác bad cân 3 tia phân giác của bha cắt bc tại e chứng minh ab+acbc+de
Đọc tiếp
cho tam giác abc c vuông tại a kẻ ah vuông góc bc tia phân giác của góc hac cắt bc tại d qua d kẻ dk vuông góc ac 1 chứng minh tam giác hac = khd 2 chứng minh tam giác bad cân 3 tia phân giác của bha cắt bc tại e chứng minh ab+ac=bc+de
1: Sửa đề: ΔAHD=ΔAKD
Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
2: góc BAD+góc CAD=90 độ
góc BDA+góc HAD=90 độ
mà góc CAD=góc HAD
nên góc BAD=góc BDA
=>ΔBAD cân tại B
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC.Kẻ AH vuông góc với BC tại H.Trên tia đối của tia HA lấy điểm M sao cho HM=HA
a)Chứng minh BA=BM và AB+AC>AM
b)Tia phân giác của góc HAC cắt HC tại O.Từ O kẻ đường thẳng song song với MC,cắt AM tại K.Chứng minh tam giác OKM là tam giác cân
Giúp mình với mn mình cảm ơn
a: Xet ΔBAM có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAM cân tại B
=>BA=BM
b: góc BAO+góc CAO=90 độ
góc BOA+góc OAH=90 độ
mà góc CAO=góc OAH
nên góc BAO=góc BOA
nên ΔBAO cân tại B
=>BA=BO=BM
=>BO=BM
Xét ΔBAC và ΔBMC có
BA=BM
góc ABC=góc MBC
BC chung
=>ΔBAC=ΔBMC
=>góc BMC=90 độ
=>OK vuông góc BM
góc KOM+góc BOK=góc BOM
góc KMO+góc BMH=góc BMO
mà góc BOK=góc BMH; góc BOM=góc BMO
nên góc KOM=góc KMO
=>ΔKMO cân tại K
Đúng 1
Bình luận (0)
Cho tam giác vuông ABC tại A, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác góc B và góc HAC cắt nhau tại I.
Chứng minh rằng A I B ^ = 90 °
Cho tam giác vuông ABC tại A, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác góc B và góc HAC cắt nhau tại I.
Chứng minh rằng A I B ^ = 90 °
Cho tam giác ABC vuông tại A ( AB<AC ) , kẻ AH vuông góc với BC , phân giác góc HAC cắt BC tại D . Chứng minh tam giác ABD là tam giác cân .
cho tam giác vuông ABC tại A, kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác góc B và góc HAC cắt nhau tại I. Chứng minh rằng góc AIB=90 độ
cho tam giác abc c vuông tại a kẻ ah vuông góc bc tia phân giác của góc hac cắt bc tại d qua d kẻ dk vuông góc ac tia phân giác của bha cắt bc tại e chứng minh ab+ac=bc+de
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc
H
A
B
^
cắt BC tại D, tia phân giác của góc
H
A
C
^
cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc H A B ^ cắt BC tại D, tia phân giác của góc H A C ^ cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.