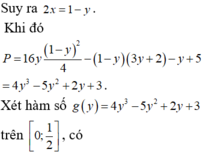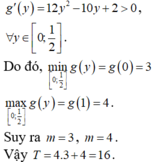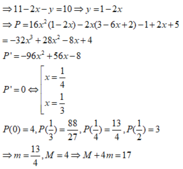cho x phần 2 = y + 8 và y - 2x = 4 giá trị của x và y lần lượt là

Những câu hỏi liên quan
y= {x2-2x-8 khi x≤2
y= {2x-12 khi x>2
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số khi x ϵ [1;-4] . Tính M+m
y= {x2-2x-8 khi x≤2
y= {2x-12 khi x>2
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số khi x ϵ [-1;4] . Tính M+m
Xét trên \(\left[-1;2\right]\Rightarrow y=x^2-2x-8\) có \(-\dfrac{b}{2a}=1\)
\(y\left(-1\right)=-5;y\left(1\right)=-9;y\left(2\right)=-8\)
Xét trên \((2;4]\Rightarrow y=2x-12\)
\(y\left(4\right)=-4\)
So sánh các giá trị trên, ta được \(M=-4;m=-9\)
\(\Rightarrow M+m=-13\)
Đúng 0
Bình luận (1)
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
2
, và
log
(
11
-
2
x
-
y
)
2...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 2 , và log ( 11 - 2 x - y ) = 2 y + 4 x - 1 . Xét biểu thức P = 16 y x 2 - 2 x ( 3 y + 2 ) - y + 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của T = ( 4 m + M ) bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hai số thực
x
,
y
thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
(
11
-
2
x
-
y
)
2
x
+
4
y
-
1
...
Đọc tiếp
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-20 và (Q): x+ny+2z+80 song với nhau. Giá trị của m và n lần lượt là : A. 4 và
1
2
B. 2 và
1
2
C. 2 và
1
4
D. 4 và
1
4
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-2=0 và (Q): x+ny+2z+8=0 song với nhau. Giá trị của m và n lần lượt là :
A. 4 và 1 2
B. 2 và 1 2
C. 2 và 1 4
D. 4 và 1 4
Đáp án A
Phương pháp : Cho hai mặt phẳng có phương trình lần lượt là :
![]()
![]()
Khi đó (P) và (Q) song song với nhau
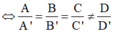
Cách giải:
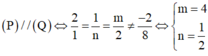
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x+y+mz-2=0 và (Q): x+ny+2z+8=0 song với nhau. Giá trị của m và n lần lượt là :
A. 4 và 1/2
A. 2 và 1/2
C. 2 và 1/4
D. 4 và 1/4
Đáp án A
Phương pháp : Cho hai mặt phẳng có phương trình lần lượt là :
(P): Ax+By+Cz+D = 0, (Q): A’x+B’y+C’z+D = 0.
Khi đó (P) và (Q) song song với nhau
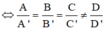
Cách giải:
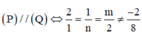
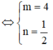
Đúng 0
Bình luận (0)
Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
y
≤
1
và
log
11
−
2
x
−
y
2
y...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Đáp án C
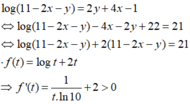
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)
Biết -2/6< x/-36 < 5/y < 2/-8 . Giá trị của x và y lần lượt là....
Ta có: \(-\frac{2}{6}< \frac{x}{-36}< \frac{2}{-8}\)
Quy đồng mẫu số ta được: \(-\frac{24}{72}< -\frac{2x}{72}< -\frac{18}{72}\)
Suy ra \(x=10\)hoặc \(x=11\).
Với \(x=10\): \(\frac{10}{-36}< \frac{5}{y}< \frac{2}{-8}\)
Quy đồng tử số ta được: \(\frac{10}{-36}< \frac{10}{2y}< \frac{10}{-40}\)
Suy ra \(y=19\).
Với \(x=11\): \(\frac{11}{-36}< \frac{5}{y}< \frac{2}{-8}\)
Quy đồng tử số ta được: \(\frac{110}{-360}< \frac{110}{22y}< \frac{110}{-440}\)
\(\Rightarrow-440< 22y< -360\Rightarrow y\in\left\{-17,-18,-19\right\}\).
Cho hai số thực x,y thỏa mãn
0
≤
x
≤
1
2
,
0
≤
y
≤
1
và
log
11
-
2
x
-
y
2
y
+
4
x
-
1
. Xét biểu thức
P
16
x...
Đọc tiếp
Cho hai số thực x,y thỏa mãn 0 ≤ x ≤ 1 2 , 0 ≤ y ≤ 1 và log 11 - 2 x - y = 2 y + 4 x - 1 . Xét biểu thức P = 16 x 2 y - 2 x 3 y + 2 - y + 5 . Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
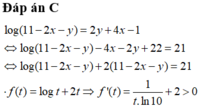
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17
Đúng 0
Bình luận (0)