CMR: tồn tại duy nhất một cặp (x;y) thỏa mãn:\(x^2-2y^2\)=1, với x,y là số nguyên tố .tìm cặp số (x;y) đó

Những câu hỏi liên quan
Chứng minh rằng tồn tại một cặp số duy nhất (x, y) thỏa mãn phương trình:
\(x^2-4x+y-6\sqrt{y}+13=0\)
Đề bài sai
Chỉ tồn tại duy nhất cặp x;y thỏa mãn pt khi đề bài là:
\(x^2-4x+y-6\sqrt{y}+13=0\)
Đúng 1
Bình luận (0)
ĐKXĐ: ...
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y-6\sqrt{y}+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(\sqrt{y}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\\sqrt{y}-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=9\end{matrix}\right.\)
Vậy có duy nhất cặp số (x;y)=(2;9) thỏa mãn phương trình
Đúng 1
Bình luận (1)
ĐK: \(y\ge0\)
\(x^2-4x+y-6\sqrt{y}+13=0\)
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y-6\sqrt{y}+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(\sqrt{y}-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=9\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)=\left(2;9\right)\) là nghiệm duy nhất của phương trình
Đúng 1
Bình luận (0)
Chứng minh rằng tồn tại duy nhất một cặp số (x,y) thỏa mãn phương trình \(x^2-4x+y-6\sqrt{y}+13=0\)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m n...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. 10 - 2 2
B. 10 + 2
C. 10 + 2 2
D. 10 - 2
Trong tất cả các cặp (x; y) thỏa mãn
log
x
2
+
y
2
+
2
(
4
x
+
4
y
-
4
)
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho
x
2
+
y...
Đọc tiếp
Trong tất cả các cặp (x; y) thỏa mãn log x 2 + y 2 + 2 ( 4 x + 4 y - 4 ) ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. ( 10 - 2 ) 2
B. 10 + 2
C. ( 10 + 2 ) 2
D. 10 - 2
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 - 2 h o ặ c 10 + 2
C. 10 - 2 2 h o ặ c 10 + 2 2
D. 10 - 2
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
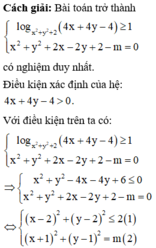

Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
2
x
-
4
y
+
6
≥
1
, tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 2 x - 4 y + 6 ≥ 1 , tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 13 - 3 v à 13 + 3
B. 13 - 3
C. 13 - 3 2
D. 13 - 3 2 và 13 + 3 2
Trong tất cả các cặp (x;y) thỏa mãn
l
o
g
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
Tìm m để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn l o g x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
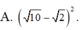
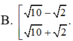
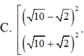
![]()
Chứng minh rằng tồn tại duy nhất cặp số (x; y) thoả mãn:\(x^2-2y^2=1\)(với x, y là các số nguyên tố). Tìm cặp số (x; y) đó
\(Giải.\)
\(x^2-2y^2=1\Leftrightarrow x^2-1=2y^2\Leftrightarrow\left(x+1\right)\left(x-1\right)=2y^2\left(chẵn\right)\)
Dễ thấy: x+1-(x-1)=2 nên 2 số trên cùng chẵn hoặc cùng lẻ=> 2 số trên cùng chẵn
=> 2y2 chia hết cho 4=>y2 chia hết cho 2
=> y chẵn =>y=2=>x2-8=1=>x=3 (thỏa mãn)
Vậy chỉ có duy nhất 1 cặp: (x,y)=(3;2) thỏa mãn
Đúng 0
Bình luận (0)
Dễ thấy: x+1-(x-1)=2 nên 2 số trên cùng chẵn hoặc cùng lẻ=> 2 số trên cùng chẵn
=> 2y2 chia hết cho 4=>y2 chia hết cho 2
=> y chẵn =>y=2=>x2-8=1=>x=3 (thỏa mãn)
Vậy chỉ có duy nhất 1 cặp: (x,y)=(3;2) thỏa mãn
Đúng 0
Bình luận (0)















