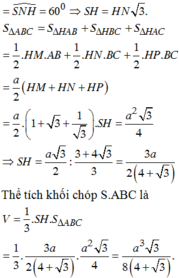Tính S của tất cả các hình tam giác trong hình bên, biết S vuông là 156,25cm2.
Đọc tiếp
Tính S của tất cả các hình tam giác trong hình bên, biết S vuông là 156,25cm2.
Những câu hỏi liên quan
cho hình vuông. Nối trung điểm hai cạch liên tiếp của hình vuông đó với nhau ta được hình vuông thứ hai. Nối trung điểm hai cạnh liên tiếp của hình vuông thứ hai với nhau ta được hình vuông thứ ba. Nối hai đường chéo của hình vuông đã cho. tính tổng diện tích tất cả các tam giác có trong hình vẽ, biết diện tích hình vuông đã cho là 156,25cm2.
cho một hình vuông. nối trung điểm 2 cạnh liên tiếp của hình vuông đó với nhau ta được hình vuông thứ 2. nối trung điểm 2 cạnh liên tiếp của hình vuông thứ 2 với nhau ta được hình vuông thứ 3. nối 2 đường chéo của hình vuông đã cho ta được hình như hình vẽ sau:
tính tổng diện tích tất cả các tam giác có trong hình vẽ. biết diện tích hình vuông đã cho là 156,25cm2
diện tích tất cả tam giác gấp 5 lần diện tích hình vuông.
Ta có : 156,25 x 5 = 781,25 (cm2)
Đúng 0
Bình luận (0)
Trong hình bên, biết cạnh của hình vuông ABCD là 9 cm . Tính s hình tròn .
( gợi ý : s hình tam giác AOB = nửa tích 2 bán kính của hình tròn tâm O ).
Diện tích hình tam giác AOB là:
9 x 9 : 2 = 40,5 (cm2)
Tích 2 bán kính là:
40,5 x 2 = 81 (cm)
Diện tích của hình tròn là:
81 x 3,14 = 245,34 (cm2)
Đáp số: 245,34 cm2
Đúng 4
Bình luận (0)
Diện tích hình tam giác AOB là:
9 x 9 : 2 = 40,5 (cm2)
Tích 2 bán kính là:
40,5 x 2 = 81 (cm)
Diện tích của hình tròn là:
81 x 3,14 = 245,34 (cm2)
Đáp số: 245,34 cm2
Đúng 0
Bình luận (0)
Trong hình bên , biết cạnh của hình vuông ABCD là 9 cm . tính s hình tròn.
( Gợi ý :s hình tam giác AOB =nửa tích 2 bán kính của hình tròn tâm O).
Tính tổng diện tích tất cả các tam giác có trong hình vẽ. Biết diện tích hình vuông đã cho là 156,25.
Trả lời: Tổng diện tích tất cả các tam giác có trong hình vẽ là
Tìm diện tích của hình vuông ABCD biết tổng tất cả các hình tam giác ở trong hình là 1704cm2
Biết có tất cả 4 hình tam giác
Một kim tự tháp được xây dựng dạng hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân biết cạnh bên và cạnh đáy của hình chóp lần lượt là 120m và 140m. thể tích của hình chóp được tính theo công thức S=1/3S.h trong đó S là diện tích đáy, h là chiều cao hình chóp. Tính chiều cao và thể tích của kim tự tháp trên.
SGK Toán 8 tập 1 – Chân trời sáng tạo
21 tháng 7 2023 lúc 21:02
Trong các phát biểu sau, phát biểu nào đúng?
Hình chóp tứ giác đều có:
A. các mặt bên là tam giác đều
B. tất cả các cạnh bằng nhau
C. các cạnh bên bằng nhau và đáy là hình vuông
D. các mặt bên là tam giác vuông
Hình chóp tứ giác có tất cả các cạnh bằng nhau - B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc lần lượt là
30
°
;
45
°
;
60
°
Tính thể tích của khối chóp S.ABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC
A
.
V
a
3
3...
Đọc tiếp
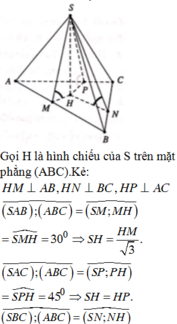
Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc lần lượt là 30 ° ; 45 ° ; 60 ° Tính thể tích của khối chóp S.ABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC
A . V = a 3 3 8 ( 4 + 3 )
B . V = a 3 3 ( 4 + 3 )
C . V = a 3 3 4 ( 4 + 3 )
D . V = a 3 3 2 ( 4 + 3 )
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a Các mặt bên (SAB),(SAC),(SBC) lần lượt tạo với đáy các góc lần lượt 30 độ, 45 độ, 60 độ Tính thể tích V của khối chóp S.ABC biết rằng hình chiếu vuông góc của S trên mặt phẳng (ABC) nằm bên trong tam giác ABC. A.
V
a
3
3
4
+...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a Các mặt bên (SAB),(SAC),(SBC) lần lượt tạo với đáy các góc lần lượt 30 độ, 45 độ, 60 độ Tính thể tích V của khối chóp S.ABC biết rằng hình chiếu vuông góc của S trên mặt phẳng (ABC) nằm bên trong tam giác ABC.
A. V = a 3 3 4 + 3
B. V = a 3 3 2 4 + 3
C. V = a 3 3 4 4 + 3
D. V = a 3 3 8 4 + 3
