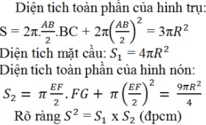chứng minh diện tích cửa tam giác đều ngoại tiếp đương tròn bán kính r bằng 3 căn 3 r bình

Những câu hỏi liên quan
chứng minh diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2
Xem chi tiết
Ta thấy bán kính đường tròn ngoại tiếp thì bằng √3232 cạnh.
Nên cạnh của tam giác gấp 2√323 bán kính, tức là bằng 2√3r23�.
Diện tích
Đúng 0
Bình luận (0)
Để chứng minh diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2, ta sẽ sử dụng các công thức và tính chất của tam giác đều và đường tròn.
Giả sử tam giác đều ngoại tiếp đường tròn có tâm O và bán kính r. Đường tròn này cắt tam giác đều tại các đỉnh A, B và C.
Để tính diện tích của tam giác đều ABC, ta sẽ sử dụng công thức diện tích tam giác đều:
Diện tích tam giác đều ABC = (cạnh)^2 * sqrt(3) / 4
Với tam giác đều ngoại tiếp đường tròn, cạnh tam giác bằng đường kính của đường tròn, tức là 2r.
Diện tích tam giác đều ABC = (2r)^2 * sqrt(3) / 4
= 4r^2 * sqrt(3) / 4
= r^2 * sqrt(3)
Vậy diện tích của tam giác đều ngoại tiếp đường tròn bán kính r là r^2 * sqrt(3).
Để chứng minh r^2 * sqrt(3) = 3r^2, ta sẽ sử dụng tính chất của căn bậc hai:
sqrt(3) = sqrt(3) * sqrt(1) = sqrt(3 * 1) = sqrt(3) * sqrt(3) / sqrt(3) = 3 / sqrt(3)
Vậy r^2 * sqrt(3) = r^2 * (3 / sqrt(3)) = 3r^2.
Vậy ta đã chứng minh được diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2.
Đúng 0
Bình luận (5)
cho tam giác ABC có bán kính đường tròn ngoại tiếp bằng 1,thỏa sinA/mA+sinB/mB+sinC/mC=căn 3.chứng minh tam giác ABC đều
Cho tam giác ABC có Â=60° bán kính đường tròn ngoại tiếp , nội tiếp tam giác ABC lần lượt lac R=7/√3 , r=√3. Tính diện tích của ∆ABC
Gọi R và r theo thứ tự là bán kính của đường tròn ngoại tiếp và đường tròn nội tiếp tam giác vuông có diện tích S. Chứng minh rằng:
\(R+r\ge\sqrt{2S}\)
Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp. r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng: AB + AC = 2(R + r)

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)
Đúng 0
Bình luận (0)
Diện tích tam giác đều ABC ngoại tiếp đường tròn tâm I,bán kính mũ 4 căn 3 bằng ........?
(Nhập kết quả dưới dạng số thập phân gọn nhất)
Diện tích tam giác đều ABC ngoại tiếp đường tròn tâm I,bán kính 4 căn 3 bằng ........?
(Nhập kết quả dưới dạng số thập phân gọn nhất)
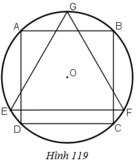
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AC 20cm, HB 9cm. Tính HC2. Cho hình thoi ABCD có cạnh 10cm, góc A bằng 60°. Tinh diện tích hình thoi ABCD3. Cho tam giác ABC vuông tại A, vẽ đường tròn nội tiếp và đường tròn ngoại tiếp tam giác ABC lần lượt có bán kính r,R. Chứng minh AB + AC 2(r + R)4. Cho tam giác ABC có góc BAC bằng 120°. Chứng minh BC^2 AB^2 + AC^2 + AB.AC5. Cho đường thẳng (d) : y ax + 3 (a khác 0). Cho biết khoảng cách từ gốc tọa độ đến (d) là frac{sqrt{ }}{ } (3 că...
Đọc tiếp
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20cm, HB = 9cm. Tính HC
2. Cho hình thoi ABCD có cạnh 10cm, góc A bằng 60°. Tinh diện tích hình thoi ABCD
3. Cho tam giác ABC vuông tại A, vẽ đường tròn nội tiếp và đường tròn ngoại tiếp tam giác ABC lần lượt có bán kính r,R. Chứng minh AB + AC = 2(r + R)
4. Cho tam giác ABC có góc BAC bằng 120°. Chứng minh BC^2 = AB^2 + AC^2 + AB.AC
5. Cho đường thẳng (d) : y = ax + 3 (a khác 0). Cho biết khoảng cách từ gốc tọa độ đến (d) là \(\frac{\sqrt{ }}{ }\) (3 căn 2)/2. Xác định a
Tìm ba phân số khác nhau biết phân số thứ nhất và phân số thứ hai là 7/8,tổng của phân số thứ hai và phân số thứ ba là 8/7,tổng của phân số thứ nhất và phân số thứ ba là 8/9
Đúng 0
Bình luận (0)