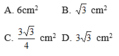Ta thấy bán kính đường tròn ngoại tiếp thì bằng √3232 cạnh.
Nên cạnh của tam giác gấp 2√323 bán kính, tức là bằng 2√3r23�.
Diện tích
Để chứng minh diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2, ta sẽ sử dụng các công thức và tính chất của tam giác đều và đường tròn.
Giả sử tam giác đều ngoại tiếp đường tròn có tâm O và bán kính r. Đường tròn này cắt tam giác đều tại các đỉnh A, B và C.
Để tính diện tích của tam giác đều ABC, ta sẽ sử dụng công thức diện tích tam giác đều:
Diện tích tam giác đều ABC = (cạnh)^2 * sqrt(3) / 4
Với tam giác đều ngoại tiếp đường tròn, cạnh tam giác bằng đường kính của đường tròn, tức là 2r.
Diện tích tam giác đều ABC = (2r)^2 * sqrt(3) / 4
= 4r^2 * sqrt(3) / 4
= r^2 * sqrt(3)
Vậy diện tích của tam giác đều ngoại tiếp đường tròn bán kính r là r^2 * sqrt(3).
Để chứng minh r^2 * sqrt(3) = 3r^2, ta sẽ sử dụng tính chất của căn bậc hai:
sqrt(3) = sqrt(3) * sqrt(1) = sqrt(3 * 1) = sqrt(3) * sqrt(3) / sqrt(3) = 3 / sqrt(3)
Vậy r^2 * sqrt(3) = r^2 * (3 / sqrt(3)) = 3r^2.
Vậy ta đã chứng minh được diện tích của tam giác đều ngoại tiếp đường tròn bán kính r bằng 3r^2.