Tam giác MNP có các cạnh MN, NP, MP lần lượt tỉ lệ với 3; 4; 5 và chu vi của tam giác MNP là 60cm. Số đo các cạnh MN, NP, MP theo thứ tự là

Những câu hỏi liên quan
Cho tam giác MNP. Từ một điểm Q trên cạnh NP, kẻ các đường song song với cạnh MN, MP lần lượt tại E, F. Chứng minh
a) tam giác ENQ đồng dạng tam giác MNP; tam giác FQP đồng dạng với tam giác MNP
b) ME/MN+MF/MP=1
Cho tam giác MNP vuông tại M,MN=3cm,MP=4cm. I là trung điểm NP. Qua I kẻ đường thẳng vuông góc với NP cắt MP,MN lần lượt ở D và E.
a) tam giác MNP đồng dạng với tam giác IDP
b) Tính các cạnh của tam giác IDP
Cho hình tam giác MNP có hai cạnh MN và MP lần lượt là 3cm , 4cm.Tính độ dài đoạn NP?
Cho tam giác MNP có MN = 12 cm, MP = 15 cm, NP =18cm, Trên các cạnh MN, MP lấy lần lượt R, S sao cho MR= 10cm và MS = 8 cm. Tính đô dài đoạn thẳng RS
Giúp mình với mọi người~~~
Hic TvT
Cho tam giác MNP, đường thẳng d song song với NP cắt hai cạnh MN và MP lần lượt tại R và Q. Chu vi tam giác MNP là 60cm và chu vi tam giác MQR là 20cm, PN = 12cm . Tính RQ?
A. 2cm
B. 2,5cm
C. 3cm
D. 4cm
Xét tam giác MNP có QR // NP , áp đụng hệ quả định lí Ta- let ta có:
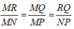
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

Chọn đáp án D
Đúng 0
Bình luận (0)
cho tam giác MNP ( MN < MP ). cho đường cao MH . gọi K,L,E lần lượt là trung điểm của các cạnh MN, MP,NP
CMR tứ giác NKLE là hình bình hành
tứ giác LEHK là hình thang cân
Giúp mik vs:(( mai mik kt r
một tam giác ABC có diện tích = 240 cm^2Gọi M, N , P lần lượt là trung điểm của các cạnh AB,AC,CB.
Nối MN,MP,NP.
tính diện tích các tam giác AMN, CNP,BMP và MNP
Nối AP vì P là truing điểm của BC nên BP = PC .
Tương tự AN = NC; AM = MB
Hai tam giác ABP và APC có đáy bằng nhau và chung chiều cao nên diện tích của chúng bằng nhau và bằng : 240 : 2 = 120 ( cm2 )
Hai tam giác PAN và PNC có đáy bằng nhau và chung chiều cao nên \(S_{PAN}=S_{PNC}=120:2=60\left(cm^2\right)\)
Tương tự ta cũng có \(S_{PAM}=S_{PBM}=60cm^2\)
Như vậy,ta có : \(S_{PNC}=S_{PBM}=60cm^2\)
Nối BN, lí luận tương tự được : \(S_{PNC}=S_{MAN}=60cm^2\)
Ta có : \(S_{MNP}=S_{ABC}-\left(S_{PNC}+S_{MAN}+S_{PMB}\right)=240-\left(60+60+60\right)=60cm^2\)
Vậy 4 tam giác có diện tích bằng nhau và bằng 60cm2
Bài 6:Cho tam giác MNP có MN = 12cm, NP = 18cm, MP = 20cm. Lấy A, B, C lần lượt là trung điểm của MN, NP, MP. Tính độdài các đoạn AB, BC, AC
+cac ban giup minh ho nha .
Xét ΔMNP có
A là trung điểm của MN
B là trung điểm của NP
Do đó: AB là đường trung bình của ΔMNP
Suy ra: \(AB=\dfrac{MP}{2}=\dfrac{20}{2}=10\left(cm\right)\)
Xét ΔMNP có
B là trung điểm của NP
C là trung điểm của MP
Do đó: BC là đường trung bình của ΔMNP
Suy ra: \(BC=\dfrac{MN}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Xét ΔMNP có
A là trung điểm của MN
C là trung điểm của MP
Do đó: AC là đường trung bình của ΔMNP
Suy ra: \(AC=\dfrac{NP}{2}=\dfrac{18}{2}=9\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác MNP vuông tại M vẽ đường cao MH, biết MN =3cm, MP = 4cm
a/ Chứng minh ∆HNM ~ ∆MNP
b/ Tính NP , MH , NH.
c/ Gọi I và K lần lượt hình chiếu của điểm H lên cạnh MN, MP.
a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
c; Đề bài yêu cầu gì?
Đúng 0
Bình luận (0)














