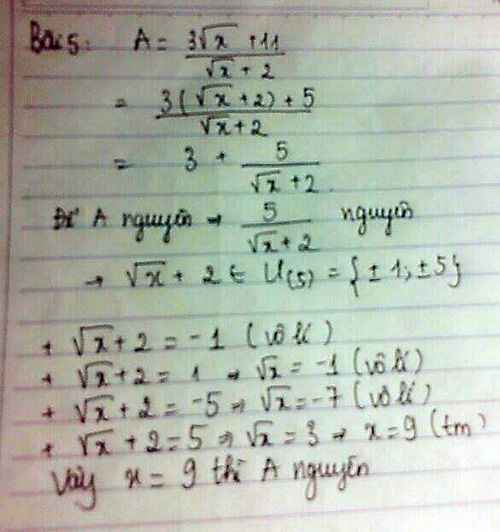\(x=\sqrt{31-8\sqrt{15}}=\sqrt{\left(4-\sqrt{15}\right)^2}=4-\sqrt{15}\)

Biểu thức nghịch đảo của x là \(\dfrac{1}{4-\sqrt{15}}=4+\sqrt{15}\)

\(\Rightarrow x=4\pm\sqrt{15}\) là nghiệm PT \(x^2+bx+c\left(1\right)\)

Đặt \(\left\{{}\begin{matrix}S=x_1+x_2\\P=x_1x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S=8\\P=1\end{matrix}\right.\) (x₁ và x₂ là nghiệm của (1))

Áp dụng Viet đảo thì x là nghiệm của PT \(x^2-8x+1\)

Vậy \(b=-8;c=1\)

Bạn có thể làm thế này:

\(x=4-\sqrt{15}\)

Giả sử \(x=4-\sqrt{15}\) là nghiệm của PT \(x^2+bx+c=0\)

\(\Leftrightarrow\left(4-\sqrt{15}\right)^2+b\left(4-\sqrt{15}\right)+c=0\\ \Leftrightarrow31-8\sqrt{15}+4b-b\sqrt{15}+c=0\\ \Leftrightarrow\sqrt{15}\left(b+8\right)=-\left(4b+c+31\right)\)

Vì b,c hữu tỉ nên \(\sqrt{15}\left(b+8\right)\) hữu tỉ

\(\Leftrightarrow\left\{{}\begin{matrix}b+8=0\\4b+c+31=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-8\\c=1\end{matrix}\right.\)

\(x-2\sqrt{x}=0\)

\(\Leftrightarrow\left(\sqrt{x}\right)^2-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(\Rightarrow\sqrt{x}=0\) và \(\sqrt{x}-2=0\)

\(\Rightarrow x=0\) và \(\sqrt{x}=2\)

\(\Rightarrow x=0\) và \(x=4\)

\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(x-2\sqrt{x}=0\)

\(\Leftrightarrow\left(\sqrt{x}\right)^2-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(\Rightarrow\sqrt{x}=0\)và \(\sqrt{x}-2=0\)

\(\Rightarrow x=0\)và \(\sqrt{x}=2\)

\(\Rightarrow x=0\)và \(x=4\)

ĐK : \(x\ge0\)

\(x-2\sqrt{x}=0\Rightarrow x=2\sqrt{x}\)

Bình phương hai vế ta có :

\(x^2=4x\Leftrightarrow x^2-4x=0\)

\(\Rightarrow x(x-4)=0\Rightarrow\hept{\begin{cases}x=0\\x=4\end{cases}}\)

Đk:\(x\ge0\)

\(x-2\sqrt{x}=0\Leftrightarrow x=2\sqrt{x}\)

Bình phương 2 vế ta có:

\(x^2=4x\Leftrightarrow x^2-4x=0\)

\(\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}\)

x - 2\(\sqrt{x}\) = 0

<=> \(\sqrt{x}\)(\(\sqrt{x}\)- 2) = 0

<=> x = 0 hoặc x = 4

\(x-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}^2-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(\Rightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\\sqrt{x}=2\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)

\(x-2\sqrt{x}=0\)\(\Leftrightarrow x=2\sqrt{x}\)

\(\Leftrightarrow x^2=\left(2\sqrt{x}\right)^2\)\(\Leftrightarrow x^2=4x\)

\(\Leftrightarrow x^2-4x=0\)\(\Leftrightarrow x\left(x-4\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}\)( thoả mãn điều kiện )

Vậy \(x=0\)hoặc \(x=4\)

a=3√x +11/√x +2

=3(√x +2)+5/√x +2

ĐK: \(x\ge0\)

\(A=\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\Leftrightarrow A\sqrt{x}+2A=3\sqrt{x}+11\)

\(\Leftrightarrow\left(A-3\right)\sqrt{x}=11-2A\left(1\right)\)

TH1: \(A=3\Rightarrow\) Không tồn tại x thỏa mãn.

TH2: \(A\ne3\)

\(\left(1\right)\Leftrightarrow\sqrt{x}=\dfrac{11-2A}{A-3}\ge0\)

\(\Rightarrow3< A\le\dfrac{11}{2}\)

Vậy \(3< A\le\dfrac{11}{2}\) thì \(A\in Z\).

\(x-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}\)

Vậy x = 0 hoặc x = 4

\(x-2\sqrt{x}=0\)

<=> \(\sqrt{x}.\sqrt{x}-2\sqrt{x}=0\)

\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=0\\\sqrt{x}-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}\)

Lời giải:
a.

Áp dụng BĐT Bunhiacopxky:

$A^2=(\sqrt{x-1}+\sqrt{9-x})^2\leq (x-1+9-x)(1+1)=16$

$\Rightarrow A\leq 4$

Vậy $A_{\max}=4$. Giá trị này đạt tại $x=5$

b.

$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$

Để $A$ nguyên thì $\frac{5}{\sqrt{x}+2}=m$ với $m$ nguyên dương

$\Leftrightarrow \sqrt{x}+2=\frac{5}{m}$

$\sqrt{x}=\frac{5-2m}{m}$

Vì $\sqrt{x}\geq 0$ nên $\frac{5-2m}{m}\geq 0$

Mà $m$ nguyên dương nên $5-2m\geq 0$

$\Leftrightarrow m\leq 2,5$. 

$\Rightarrow m=1; 2$

$\Rightarrow x=9; x=\frac{1}{4}$