Cho tam giác đều cạnh \(5\sqrt{3}\) cm. Tính bán kính đường tròn ngoại tiếp tam giác đó

Những câu hỏi liên quan
Cho tam giác đều ABC cạnh bằng 2 cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC
Gọi O là giao 3 đường trung trực của ∆ABC. Khi đó O là tâm đường tròn ngoại tiếp ∆ABC. Gọi H là giao điểm của AO và BC. Ta có : AH = 3 cm
OA = 2 3 AH = 2 3 3 cm
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
Theo định lí sin ta có:
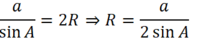
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
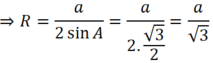
Đúng 0
Bình luận (0)
Cho ABC là tam giác đều cạnh 6 cm. Bán kính đường tròn ngoại tiếp tam giác ABC bằng
A. 3 3
B. 2 3
C. 4 3
D. 3
Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ R = a 2 sin A = 6 2. sin 60 0 = 2 3
Chọn B.
Đúng 0
Bình luận (0)
Cho MNP là tam giác đều cạnh dài 9 cm. Bán kính đường tròn ngoại tiếp tam giác MNP bằng:
Bán kính đường tròn ngoại tiếp tam giác MNP bằng: 3 3 cm
Đúng 0
Bình luận (0)
Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
A. 2 3 cm B. 2cm C. 3 cm D. 2 cm
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
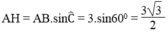
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
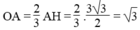
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
Cho tam giác đều cạnh 4. Tính bán kính đường tròn ngoại tiếp tam giác ABC
cho tam giác đều ABC và đường tròn nội tiếp nó.có bán kính là 1 cm .tính bán kính đường tron ngoại tiếp tam giác ABC
Gọi cạnh tam giác ABC là x
theo công thức tính diện tích S = p.r với p là nửa chu vi, r là bán kính đường tròn nội tiếp.
Ta có \(\frac{x^2\sqrt{3}}{4}=\frac{3x}{2}.1\Rightarrow x=2\sqrt{3}\) (cm)
Suy ra bán kính đường tròn ngoại tiếp : \(R=\frac{AB.BC.AC}{4.S_{ABC}}\frac{x^3}{\frac{4.x^2\sqrt{3}}{4}}=\frac{x}{\sqrt{3}}=2\) (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC đều có cạnh bằng 6 cm.Tính bán kính của đường tròn ngoại tiếp tam giác đó.
Cho tam giác đều ABC có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
Bán kính đường tròn ngoại tiếp của ΔABC là:
Đúng 0
Bình luận (0)
\(R=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)













