Theo định lí sin ta có:
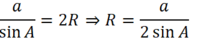
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
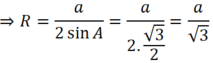
Theo định lí sin ta có:
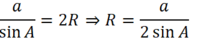
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
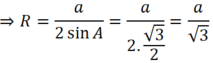
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
A. a 3 3
B. a 3 2
C. a 3 4
D. a 2 2
Cho ABC là tam giác đều cạnh 6 cm. Bán kính đường tròn ngoại tiếp tam giác ABC bằng
A. 3 3
B. 2 3
C. 4 3
D. 3
Cho tam giác ABC cân đỉnh A, ^A=α, AB=m, D là một điểm trên cạnh BC sao cho BC=3BD
a) Tính BC, AD
b) Chứng tỏ rằng đường tròn ngoại tiếp các tam giác ABD, ACD là bằng nhau. Tính cosα để bán kính chúng bằng 1/2 bán kính R của đường tròn ngoại tiếp tam giác ABC
Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
Cho tam giác ABC có góc B = 45 độ, cạnh AC = \(2\sqrt{2}\) cm. Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng
Cho tam giác ABC có a = 5, b = 7, c = 8. Bán kính đường tròn ngoại tiếp tam giác bằng
A. 7 3
B. 7 3 3
C. 7 5 3
D. 7 2 3
Ví dụ 1. Tam giác ABC có các cạnh a = 13 m, b = 14 m và c = 15 m a) Tính diện tích tam giác ABC ; b) Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác ABC. Ví dụ 2. Tam giác ABC có cạnh a = 2√3 , cạnh b = 2 và C (mũ) = 30⁰. Tính cạnh c, góc A và diện tích tam giác đó. Ví dụ 3. Cho tam giác ABC có cạnh a = 24cm b = 13cm và c = 15vm .Tính diện tích S của tam giác và bán kính r của đường tròn nội tiếp, 1. Cho tam giác ABC vuông tại A,B = 58⁰ và cạnh a = 72cm Tính C (mũ), cạnh bạcạnh c và đường cao ha 2. Cho tam giác ABC biết các cạnh a = 52.1 cm, b = 85 cm và c = 54 cm. Tính các góc A(mũ), B(mũ) và C(mũ).
Cho tam giác ABC, biết góc góc A bằng 600, AC = 8cm, AB = 5cm. Tính bán kính R đường tròn ngoại tiếp tam giác ABC.
A. 4,4
B. 4,04
C. 3,84
D. 5,02