2. Vẽ sơ đồ khối giải bất phương trình mx+n

Những câu hỏi liên quan
hãy vẽ sơ đồ khối miêu tả thuật toán giải phương trình bậc nhất ax+b=0
vẽ sơ đồ khối trình bày bài toán : tìm giá trị lớn nhất , nhỏ nhất của 3 số bất kì
#include <bits/stdc++.h>
using namespace std;
double a,b,c;
int main()
{
cin>>a>>b>>c;
cout<<"So lon nhat la:"<<fixed<<setprecision(2)<<max(a,max(b,c))<<endl;
cout<<"So nho nhat la:"<<fixed<<setprecision(2)<<min(a,min(b,c));
return 0;
}
Đúng 0
Bình luận (0)
vẽ sơ đồ khối trình bày bài toán : tìm giá trị lớn nhất , nhỏ nhất của 3 số bất kì
#include <bits/stdc++.h>
using namespace std;
double ln,nn,a,b,c;
int main()
{
cin>>a>>b>>c;
ln=max(a,max(b,c));
nn=min(a,min(b,c));
cout<<fixed<<setprecision(2)<<ln<<endl;
cout<<fixed<<setprecision(2)<<nn<endl;
return 0;
}
Đúng 0
Bình luận (1)
1. Xác định bài toán và thuật toán giải bất phương trình mx+n
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để bất phương trình
m
x
+
m
2
5
-
x
2
+
2
m
+
1
f
x
≥...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để bất phương trình m x + m 2 5 - x 2 + 2 m + 1 f x ≥ 0 nghiệm đúng với mọi x ∈ - 2 ; 2 ?

A. 1
B. 3
C. 0
D. 2
Giải bất phương trình: \(mx\left(x+1\right)>mx\left(x+m\right)+m^2-1.\)
\(mx.\left(x+1\right)>mx.\left(x+m\right)+m^2-1\Leftrightarrow mx^2+mx>mx^2+m^2x+m^2-1\Leftrightarrow mx>m^2x+m^2-1\\ \).
\(\Leftrightarrow mx-m^2x-m^2+1>0\Leftrightarrow mx.\left(1-m\right)+\left(1-m\right).\left(1+m\right)>0\)
\(\Leftrightarrow\left(1-m\right).\left(mx+1+m\right)>0\)
+ Nếu \(m>1\Rightarrow1-m< 0\Rightarrow mx+1+m< 0\Leftrightarrow m.\left(x+1\right)< -1\)
Mà \(m>1\Rightarrow x+1< -\frac{1}{1}=-1\Leftrightarrow x< -2\)
+ Nếu m<1 thì làm tiếp
Đúng 0
Bình luận (0)
Em hãy mô tả thuật toán giải phương trình bậc nhất ax + b = 0 (bằng liệt kê các bước hoặc bằng sơ đồ khối).
Mô tả thuật toán phương trình bậc nhất ax + b = 0 như sau:
1. Nhập giá trị của a và b từ bàn phím.
2. Nếu a=0:
- Nếu b=0, phương trình vô số nghiệm
- Nếu b=0, phương trình vô nghiệm.
3. Nếu a khác 0, x = -b/a.
4. Hiển thị giá trị của x trên màn hình.
Đúng 2
Bình luận (0)
Cho hàm số
y
a
x
+
b
c
x
+
d
có đồ thị (C) như hình vẽ bên dưới. Giải bất phương trình
y
a
x
+
b
c
x
+
d
≥
1
A. ...
Đọc tiếp
Cho hàm số y = a x + b c x + d có đồ thị (C) như hình vẽ bên dưới. Giải bất phương trình y = a x + b c x + d ≥ 1
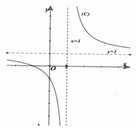
A. x ≤ - 1
B. x ≥ 1
C. x>1
D. x>-1
Hướng dẫn giải
Dựa vào đồ thị ta có, đường thẳng y =1 là đường tiệm cận ngang và x = 1 là đường tiệm cận đứng của đồ thị hàm số. Do đó :
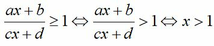
(đồ thị (C) “nằm trên” đường thẳng y =1 ứng với x>1). Chọn C
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
+
b
c
x
+
d
có đồ thị (C) như hình vẽ bên dưới. Giải bất phương trình
y
a
x
+
b
c
x
+
d
≥...
Đọc tiếp
Cho hàm số y = a x + b c x + d có đồ thị (C) như hình vẽ bên dưới. Giải bất phương trình y = a x + b c x + d ≥ 1
![]()
![]()
![]()
![]()

















