Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh các độ dài BK,BC
**
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh các độ dài BK và BC ?
vì tam giác ABC là tam giác vuông tại A
⇒góc A=900
Xét tam giác ABK có
góc A = 900⇒góc A>góc BKA⇒BK > AB
có góc BKC = góc ABK+ góc A (BKC là góc ngoài của tam giác ABD)
⇒góc BKC > góc A⇒góc BKC>900
Xét tam giác BKC có:BKC>900 ⇒BKC > C
⇒BC>BK(quan hệ giữa cạnh và góc đối diện trong 1 tam giác)
vậy BC>BK
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh độ dài BK, BC.
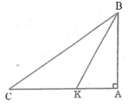
Trong ΔABK, ta có ∠BKC là góc ngoài tại đỉnh K nên ∠BKC = ∠A + ∠ABK
Suy ra: ∠BKC > ∠A = 90o (tính chất góc ngoài)
Trong ΔBKC ta có ∠BKC là góc tù, BC là cạnh đối diện với ∠BKC
Suy ra BC là cạnh lớn nhất
Do đó BC > BK.
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh độ dài BK và BC
1,cho tam giác ABC, có góc A là góc tù, góc B >góc C. So sánh các cạnh trong Tam giác ABC
2, Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh các độ dài BK,BC
nhờ mn giúp ạ ,càng nhanh càng tốt ><
\(\text{1)Vì }\Delta ABC\text{ có }A\text{ là góc tù}\)
\(\Rightarrow A\text{ lớn nhất}\)
\(\text{Vậy }\widehat{A}>\widehat{B}>\widehat{C}\)
\(\Rightarrow BC>AB>AC\)
\(\text{2)Vì }\Delta ABC\text{ vuông tại }A\)
\(\Rightarrow\widehat{A}=90^0\)
\(\text{Xét }\Delta ABK\text{ có:}\)
\(\widehat{A}=90^0\left(cmt\right)\)
\(\Rightarrow\widehat{A}>\widehat{BKA}\)
\(\Rightarrow BK>AB\)
\(\text{Ta có:}\widehat{BKC}=\widehat{ABK}+\widehat{A}\left(\widehat{BKC\text{ là góc ngoài }\Delta}ABD\right)\)
\(\Rightarrow\widehat{BKC}>\widehat{A}\)
\(\Rightarrow\widehat{BKC}>90^0\)
\(\text{Xét }\Delta BKC\text{ có:}\)
\(\widehat{BKC}>90^0\)
\(\Rightarrow\widehat{BKC}>\widehat{C}\)
\(\Rightarrow BC>BK\text{(quan hệ giữa cạnh và góc đối diện trong tam giác)}\)
1: Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB
1)So sánh các cạnh của Tam giác ABC biết A= 80° B=40°
2)Sosánh các cạnh của Tam giác PQR biết P = 70° R= 50°
3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC
4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ
5) Cho tam giác ABC có ba góc nhọn AB < AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh các độ đài BK,BC
(GIẢI CHI TIẾT CỘNG VẼ HÌNH NHA, XONG CÓ QUÀ)
tam giác abc vuông tại a. điểm k nằm giữa a và c. so sánh bk và bc
Ta có : tam giác ABC vuông tại A => A^,C^ (1)
Mặt khác:^CKB là góc ngoài tại đỉnh K của tam giác ABK
^CKB>^A (2)
Từ (1) và (2) => ^CKB>^C => BC>BK
cho tam giác abc vuông tại A .điểm I nằm giữa A và C so sánh độ dài BI và BC
góc AIB<90 độ
=>góc BIC>90 độ
Xét ΔBIC có góc BIC>90 độ
nên BC là cạnh lớn nhất
=>BC>BI
Cho tam giác ABC vuông tại A có \(\widehat B > {45^o}\)
a) So sánh các cạnh của tam giác
b) Lấy điểm K bất kì thuộc đoạn thẳng AC. So sánh độ dài BK và BC.
Tham khảo:
a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)
Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)
b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>(\widehat {BAK}=90^0\)
Xét tam giác BCK, ta có :
\(\widehat {BKC} > {90^o} > \widehat {BCK}\)
\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)