Trong mpOxy, cho tam giác ABC có A(1; 1), B(3; 3), C(0;-6).
1,Tính cos A.
2,Tìm tọa độ điểm D sao cho tam giác ABD vuông cân tại D.
3,Gọi E là chân đường phân giác trong của góc A.Tìm tọa độ điểm E.
Những câu hỏi liên quan
Trong mpOxy, cho HBH ABCD có phương trình đường chéo AC:x-y+1=0, điểm G(1;4) là trọng tâm tam giác ABC,điểm E(0;3) thuộc đường cao kẻ từ D của tam giác ACD.Tìm tọa độ các đỉnh HBH biết diện tích tứ giác AGCD bằng 32 và đỉnh A có tung độ dương.
Bài 1: Trong mpOxy cho tam giác ABC với A(0;1) B(3;2) và C(1;5). Tìm trực tâm H của tam giác ABC .
Bài 2: Trong mpOxy cho tam giác ABC với A(1;5) B(–4;–5) và C(4;-1). Tìm tâm J của đường tròn nội tiếp tam giác ABC.
Bài 3: Trong mpOxy cho tam giác ABC với A(1 ; 5) B(3;–1) C(6;0). Tìm chân đường cao B’ kẻ từ B lên CA.
Bài 1: Trong mpOxy cho tam giác ABC với A(3;–1) B(1;5) và C(6;0) . Gọi A’ là chân đường cao kẻ từ A lên BC tìm A’.
Bài 2: Trong mpOxy cho tam giác ABC với A(0;3) B(2;2) và C(–6;1). Tính số đo của góc A.
Bài 6. Trong mpOxy, cho A(−2;6), B(1;2) , C(9;8). a) Chứng minh tam giác ABC vuông. b) Gọi I là trung điểm của cạnh AC. Tìm tọa độ trực tâm H của tam giác ABI. c) Tìm tọa độ điểm E đối xứng với I qua cạnh BC.
Trong không gian Oxyz, cho các điểm
A
0
;
4
2
;
0
,
B
0
,
0
,
4
2
điểm
C
∈
m
p
O
x
y...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A 0 ; 4 2 ; 0 , B 0 , 0 , 4 2 điểm C ∈ m p O x y và tam giác OAC vuông tại C; hình chiếu vuông góc của O trên BC là điểm H. Khi đó điểm H luôn thuộc đường tròn cố định có bán kính bằng:
A. 2 2
B. 4
C. 3
D. 2
Ta có:
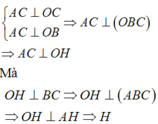
di động trên mặt cầu đường kính OA.
Mặt khác O H ⊥ B H ⇒ H di động trên mặt cầu đường kính OB.
⇒ H di động trên đường tròn cố định là giao tuyến của hai mặt cầu trên (mặt cầu đường kính OA và mặt cầu đường kính OB)
Bán kính cần tìm là:
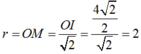
(do tam giác OIM vuông cân tại M)
Chọn D.
Đúng 0
Bình luận (0)
bài 1: cho tam giác ABC có A-B+C= 90 độ và A-C=-5 độ .So sánh cạnh trong tam giác ABC
Xem chi tiết
bài 2:cho tam giác ABC có A+B-2C=27 độ và A+3C=273 độ.So sánh các cạnh trong tam giác ABC
bài 3:cho tam giác ABC có C-3B-2A=-3 độ và 5B-2A=16 độ. Tính các góc từ đó so sánh các cạnh trong tam giác ABC
20 tháng 8 2021 lúc 17:51
Mình cần gấp ạ....
1)Cho tam giác ABC cân tại A có AB=6 cm,BC=4 cm.Tính các góc trong tam giác ABC.
2)Cho tam giác ABC vuông tại A có góc B=50 độ,BC=5 cm.Ở phía ngoài tam giác ABC,vẽ tam giác vuông ADC có góc CAD=35 độ.Tính chu vi tam giác ABC và chu vi tam giác ADC
Trong mp xOy cho tam giác ABC. bt A(3;-1) B(-1;2) I(1;-1) là trọng tâm của tam giác ABC. Trực tâm H của tam giác ABC có tọa độ (a;b). Tính a+3b
Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=1 và AC=2. Có 6 điểm thuộc tam giác ABC ( nằm trong hoặc nằm trên cạnh của tam giác ABC). CMR: tôn tại hai điểm có khoảng cách không vượt quá 1.