tìm các số nguyên x và y biết x+3y+xy=5
Bài 4. Tìm các số nguyên x và y thỏa mãn (x+1).( y-2) =5 Bài 5. Tìm các số nguyên x và y thỏa mãn xy -2x + 3y
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
Bài 1:
Tìm các số nguyên x,y biết;
a,x.(2y-1)=6y+5 b,xy-2x+3y=4
Bài 2: Tìm các số tự nhiên x,n và số nguyên tố p,q biết:
a,pq+13;5p+q đều là số nguyên tố
b,(x^2+4x+32)(x+4)
tìm các số nguyên x,y sao cho
a,2x+xy-3y=18
b,tìm các số nguyên x biết tích (x^2-5).(x^2-25) là sô nguyên âm
Ta có : 2x + xy - 3y = 18
=> x(y + 2) - 3y = 18
=> x(y + 2) - 3y - 6 = 18 - 6
=> x(y + 2) - 3(x + 2) = 12
=> (x - 3)(y + 2) = 12
Vì \(x;y\inℤ\Rightarrow\hept{\begin{cases}x-3\inℤ\\y+2\inℤ\end{cases}}\)
Lại có : 12 = 1.12 = 3.4 = 2.6 = (-1).(-12) = (-3).(-4) = (-2).(-6)
Lập bảng xét 12 trường hợp
| x - 3 | 1 | 12 | -1 | -12 | 3 | 4 | -3 | -4 | 2 | 6 | -2 | -6 |
| y + 2 | 12 | 1 | -12 | -1 | 4 | 3 | -4 | -3 | 6 | 2 | -6 | -2 |
| x | 4 | 15 | 2 | -9 | 6 | 7 | 0 | -1 | 5 | 9 | 1 | -3 |
| y | 10 | -1 | -14 | -3 | 2 | 1 | -6 | -5 | 4 | 0 | -8 | -4 |
Vậy các cặp số (x;y) nguyên thỏa mãn là : (4 ; 10) ; (15 ; - 1) ; (2 ; -14) ; (-9 ; -3) ; (6 ; 2) ; (7 ; 1) ; (0 ; -6) ; (-1 ' 5) ; (5 ; 4) ; (9 ; 0) ;
(1 ; -8) ; (-3 ; -4)
b) \(\left(x^2-5\right)\left(x^2-25\right)< 0\)
TH1 : \(\hept{\begin{cases}x^2-5>0\\x^2-25< 0\end{cases}\Rightarrow\hept{\begin{cases}x^2>5\\x^2< 25\end{cases}}\Rightarrow5< x^2< 25\Rightarrow x^2\in\left\{9;16\right\}}\)(vì x là số nguyên)
=> \(x\in\left\{\pm3;\pm4\right\}\)
TH2 : \(\hept{\begin{cases}x^2-5< 0\\x^2-25>0\end{cases}}\Rightarrow\hept{\begin{cases}x^2< 5\\x^2>25\end{cases}}\Rightarrow x\in\varnothing\)
Vậy \(x\in\left\{\pm3;\pm4\right\}\)
2x + xy - 3y = 18
<=> 2x + xy - 6 - 3y = 12
<=> ( 2x + xy ) - ( 6 + 3y ) = 12
<=> x( 2 + y ) - 3( 2 + y ) = 12
<=> ( x - 3 )( 2 + y ) = 12
Lập bảng :
| x-3 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 6 | -6 | 12 | -12 |
| x | 4 | 2 | 5 | 1 | 6 | 0 | 7 | -1 | 9 | -3 | 15 | -9 |
| 2+y | 12 | -12 | 6 | -6 | 4 | -4 | 3 | -3 | 2 | -2 | 1 | -1 |
| y | 10 | -14 | 4 | -8 | 2 | -6 | 1 | -5 | 0 | -4 | -1 | -3 |
Vậy ta có 12 cặp ( x ; y ) thỏa mãn
( 4 ; 10 ) , ( 2 ; -14 ) , ( 5 ; 4 ) , ( 1 ; -8 ) , ( 6 ; 2 ) , ( 0 ; -6 ) , ( 7 ; 1 ) , ( -1 ; -5 ) , ( 9 ; 0 ) , ( -3 ; -4 ) , ( 15 ; -1 ) , ( -9 ; -3 )
Tìm các số nguyên x , y biết: xy + 3x + 3y=-16
Lời giải:
$xy+3x+3y=-16$
$(xy+3x)+(3y+9)=-7$
$x(y+3)+3(y+3)=-7$
$(y+3)(x+3)=-7$
Vì $x,y$ nguyên nên $x+3, y+3$ nguyên. Ta có bảng sau: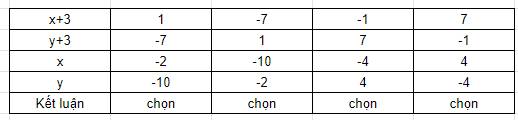
tìm các số nguyên x,y biết: xy-2x+3y=21
=>x(y-2)+3y-6=15
=>(y-2)(x+3)=15
=>\(\left(x+3;y-2\right)\in\left\{\left(1;15\right);\left(15;1\right);\left(-1;-15\right);\left(-15;-1\right);\left(3;5\right);\left(5;3\right);\left(-3;-5\right);\left(-5;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-2;17\right);\left(12;3\right);\left(-4;-13\right);\left(-18;1\right);\left(0;7\right);\left(2;5\right);\left(-6;-3\right);\left(-8;-1\right)\right\}\)
TÌM CÁC CẶP SỐ NGUYÊN x;y BIẾT :
a)xy-y=15
b)xy+3y-17=0
c)xy-3y+2x=0
Tìm các số nguyên x,y biết xy-2x+3y=3
xy - 2x + 3y = 3
x ( y - 2 ) + 3. ( y - 2 ) = 3 - 6
( x + 3 ) ( y - 2 ) = -3
ta có : -3 = 1 . ( - 3 ) = ( -1 ) . 3
sau đó bạn thử từng trường hợp ra là được
1:tìm các số nguyên x,y biết:
xy - 3y + y = 20
2:tìm các số nguyên x,thỏa mãn:
(x - 3 ).(x + 4) >0
3:Cho S=1-5+52-53+....+598-599
a)Tính S.
b) Chứng minh rằng :5100 chia cho 6 dư 1
( giúp mk với,mk đang cần gấp ^^)
Bài 2:
Ta có: (x-3)(x+4)>0
=>x>3 hoặc x<-4
Bài 3:
a: \(5S=5-5^2+...+5^{99}-5^{100}\)
\(\Leftrightarrow6S=1-5^{100}\)
hay \(S=\dfrac{1-5^{100}}{6}\)
tìm các số nguyên x;y biết: xy+7x-3y=32
đồ ngu cô ra một loạt sao ko hỏi cho hêt
Kí tên QUỐC
Thôi BYE!
NAMEUCHI MỚI NGU AK !!!... CÒN BÀI NÀY THÌ LÊ THANH BÌNH TUEJ GIẢI NHA!!!!