Cho tam giác ABC có trung tuyến AM (A thuộc BC) và BM < AM. Chứng minh: góc A nhọn

Những câu hỏi liên quan
Cho tam giác ABC có AB AC 5cm, BC 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.a) Chứng minh △AMB △AMC và AM là tia phân giác của góc A.b) Chứng minh AM BC.c) Tính độ dài các đoạn thẳng BM và AM.d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì ? Vì sao ?
Đọc tiếp
Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.
a) Chứng minh △AMB = △AMC và AM là tia phân giác của góc A.
b) Chứng minh AM ![]() BC.
BC.
c) Tính độ dài các đoạn thẳng BM và AM.
d) Từ M vẽ ME ![]() AB (E thuộc AB) và MF
AB (E thuộc AB) và MF ![]() AC (F thuộc AC). Tam giác MEF là tam giác gì ? Vì sao ?
AC (F thuộc AC). Tam giác MEF là tam giác gì ? Vì sao ?
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: BM=CM=3cm
=>AM=4cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB AC 5cm , BC 6cm.Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC a. Chứng minh tam giác AMB tam giác AMC và AM là tia phân giác của góc Ab. Chứng minh AM vuông góc BC c. Tính độ dài các đoạn thẳng BM và AM d. Từ M vẽ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Tam giác MEF là tam giác gì ? Vì sao ?~ Meo~ Giúp mình với các bạn ơi ~
Đọc tiếp
Cho tam giác ABC có AB = AC = 5cm , BC = 6cm.Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC
a. Chứng minh tam giác AMB = tam giác AMC và AM là tia phân giác của góc A
b. Chứng minh AM vuông góc BC
c. Tính độ dài các đoạn thẳng BM và AM
d. Từ M vẽ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Tam giác MEF là tam giác gì ? Vì sao ?
~ Meo~ Giúp mình với các bạn ơi ~
Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.
a) Chứng minh ΔAMB = ΔAMC và AM là tia phân giác của góc A.
b) Chứng minh AM
c) Tính độ dài các đoạn thẳng BM và AM.
d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì? Vì sao?
HELP ME
a. Xét tam giác AMB và tam giác AMC:
AB = AC
AM chung
BM = CM (trung tuyến AM hạ từ A đến BC)
=> tam giác AMB = tam giác AMC
=> góc BAM = góc CAM (2 góc tương ứng)=>AM là tia phân giác của góc BACb. đề bài bị thiếuc. ta có BM = CM(cma) => BM = CM = \(\dfrac{BC}{2}\)= \(\dfrac{6}{2}\)= 3(cm) Áp dụng định lí Pi-ta-go vào tam giác ABM: AB2 = BM2 + AM2=> AM2 = AB2 - BM2 AM2 = 52 - 32 = 25 - 9 = 16(cm)=> AM = 4 cm
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A và BAC là góc nhọn. Vẽ trung tuyến AM (M thuộc BC) . Từ M kẻ MH vuông góc AB (H thuộc AB) và MK vuông góc AC (K thuộc AC)a, Chứng minh: MH MKb, Chứng minh: AM là trung trực của HKc, Gọi I là giao điểm của AC và MH. Xác định trực tâm của tam giác AMId, Từ B kẻ Bx vuông góc BA và Cy vuông góc CA . Bx cắt Cy tại D.e, Chứng minh: A, M, D thẳng hàng e, Tính độ dài của đoạn thẳng IM khi AK 2cm và BAC 60 độ
Đọc tiếp
Cho tam giác ABC cân tại A và BAC là góc nhọn. Vẽ trung tuyến AM (M thuộc BC) . Từ M kẻ MH vuông góc AB (H thuộc AB) và MK vuông góc AC (K thuộc AC)
a, Chứng minh: MH = MK
b, Chứng minh: AM là trung trực của HK
c, Gọi I là giao điểm của AC và MH. Xác định trực tâm của tam giác AMI
d, Từ B kẻ Bx vuông góc BA và Cy vuông góc CA . Bx cắt Cy tại D.
e, Chứng minh: A, M, D thẳng hàng e, Tính độ dài của đoạn thẳng IM khi AK = 2cm và BAC= 60 độ
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM vừa là đường cao vừa là đường phân giác
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Ta có: ΔAHK cân tại A
mà AM là đường phân giác
nên AM là đường trung trực của HK
Đúng 4
Bình luận (0)
1.Cho tam giac ABC cân tại A. E,F thuộc BC sao cho BE=EF=FC
a, So sánh góc BAE,EAF,FAC
2.Cho tam giác ABC có M là trung điểm của BC nối AM. Chứng minh
a, AB>BM thì góc BAC nhọn
b, AM<BM thì BAC tù
Cho tam giác ABC có AB =AC=5cm, BC=6cm Đường trung tuyến AM xuất phát từ đỉnh Acủa tam giác ABC
a chứng minh tam giác AMB = tam giác AMC là tia phân giác của góc A
b chứng minh AM vuông BC
c tính độ dài các đọn thằng BM và AM
Giải
Xét tam giác AMB và tam giác AMC
AM chung
AB=AC(gt)
MB=MC(AM là trung tuyến của tam giác ABC)
Vậy tam giác AMB= tam giác AMC(c.c.c)
Suy ra :góc BAM = góc CAM
Suy ra AM là hân giác của gócA
Ý b
Vì tam giác AMB= tam giác AMC(cmt)
suy ra
góc AMB= góc AMC
có góc AMB+AMC=180 độ
mà góc AMB=góc AMC=90 độ
Suy ra AM vuông góc với BC
tam giác AMB vuông tại B
Ý c
Vì MB=MC=3cm
Áp dụng định lý PI-TA-GO và tam giác vuông ta có
AB^2=MB^2+MA^2
25=9+MA^2
MA^2=16
MA=4cm
Cho tam giác vuông tại A,có BM là tia phân giác của góc ABC(M thuộc AC).Kẻ MH vuông góc BC(H thuộc BC)
a)chứng minh tam giác AMB=tam giác HBM
b)chứng minh AM=HM
C)so sánh AM và MC
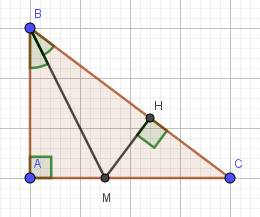
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
Đúng 2
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
Cho tam giác ABC có AB = AC = 5cm,BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh Acủa tam giác ABC
a, Chứng minh △AMB = △AMC và AM là tia phân giác của góc A
b, Chứng minh AM⊥BC
c, Tính độ dài các đoạn thẳng BM và AM
a)xét △AMB = △AMC có
AB = AC
AMchung
CM=BM(vì AM là Đường trung tuyến)
=>△AMB = △AMC(c-c-c)
=>góc BAM = góc CAM
=> AM là tia phân giác của góc A
Đúng 1
Bình luận (0)
theo c/m câu a ta có △AMB = △AMC
=>góc BMA=góc CMA
=>góc BMA=góc CMA=\(\dfrac{180}{2}=90^o\)(2 góc kề bù)
=> AM⊥BC
Đúng 1
Bình luận (0)
Xem thêm câu trả lời





















