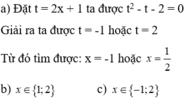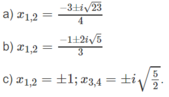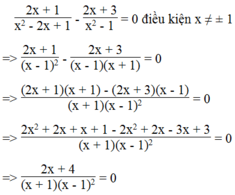
Biểu thức bằng 0 khi tử bằng 0 và mẫu khác 0

Ta có: 2x + 4 = 0 => x = - 2 (thỏa mãn điều kiện)

Vậy với x = - 2 thì giá trị của biểu thức bằng 0.

Cho mk xin yêu cầu của bài được ko vậy ???

a. 2x²-5x+1=0

△= b² - 4ac = (-5)² - 4*2*1 = 17 ⇒√△ = √17

\(\Rightarrow x_1=\frac{5+\sqrt{17}}{4};x_2=\frac{5-\sqrt{17}}{4}\)

Vậy .... S={\(\frac{5\pm\sqrt{17}}{4}\)}

b. 4x² +4x+1=0

⇔(2x+1)² = 0 ⇔ x=\(\frac{-1}{2}\)

c. -3x² +2x+8=0

△' = b'² - ac = 1² - (-3)*8 = 25 ⇒√△ = 5

\(\Rightarrow x_1=\frac{-1+5}{-3}=-\frac{4}{3};x_2=\frac{-1-5}{-3}=2\)

Vậy... S={-\(\frac{4}{3}\);2}

d. 5x2 6x1=0 (thiếu dấu nên mk chưa giải được)

e. -3x²+ 14x - 8=0

△' = b'² - ac = 7² - (-3)*(-8) = 25 ⇒ √△ = 5

⇒\(x_1=\frac{-7+5}{-3}=\frac{2}{3};x_2=\frac{-7-5}{-3}=4\)

Vậy .... S={\(\frac{2}{3};4\)}

g. -7x² +4x-3=0

△' = b'² - ac = 2² - (-7)*(-3) = -17<0

Vậy pt vô nghiệm , S=∅

3x² + 2x - 1 = 0

=> 3x² + 3x - x - 1 = 0

=> 3x(x + 1) - (x + 1) = 0

=> (3x - 1)(x + 1) = 0

=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)

x² - 5x + 6 = 0

=> x² - 2x - 3x + 6 = 0

=> x(x - 2) - 3(x - 2) = 0

=> (x - 3)(x - 2) = 0

=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)

3x² + 7x + 2 = 0

=> 3x² + 6x + x  + 2 = 0

=> 3x(x + 2) + (x + 2) = 0

=> (3x + 1)(x + 2) = 0

=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)

1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)

\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)

2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)

\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)

3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)

\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)

\(x^2-4x+1=0\)

\(\Leftrightarrow\left(x^2-4x+4\right)=3\)

\(\Leftrightarrow\left(x-2\right)^2=3\)

\(\Leftrightarrow x=\sqrt{3}+2;x=2-\sqrt{3}\)

\(2x^2-6x+1=0\)

\(\Leftrightarrow4x^2-12x+2=0\)

\(\Leftrightarrow\left(2x-3\right)^2=7\)

\(\Leftrightarrow x=\frac{\sqrt{7}+3}{2};x=\frac{3-\sqrt{7}}{2}\)

\(3x^2+4x-4=0\)

\(\Leftrightarrow3x^2-2x+6x-4=0\)

\(\Leftrightarrow\left(x+2\right)\left(3x-2\right)=0\)

\(\Leftrightarrow x=-2;x=\frac{2}{3}\)

a: Ta có: \(40x^4+5x=0\)

\(\Leftrightarrow5x\left(8x^3+1\right)=0\)

\(\Leftrightarrow x\left(2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)

b: Ta có: \(8x^2-2x-1=0\)

\(\Leftrightarrow8x^2-4x+2x-1=0\)

\(\Leftrightarrow\left(2x-1\right)\left(4x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)

\(a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x-1\right)+2\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

a) \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14y=-42\\2x+3y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

b) \(3x^2+4x=0\) 

\(\Leftrightarrow x\left(3x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy phương trình có tập nghiệm là: \(S=\left\{0;-\dfrac{4}{3}\right\}\)

c) Đặt:  \(x^2=t\left(t\ge0\right)\)

\(\Rightarrow\) Ta có phương trình mới:

\(t^2-3t-4=0\) 

Ta có: a - b + c = 1 + 3 - 4 = 0

\(\Rightarrow t_1=-1\left(loại\right);t_2=4\left(TM\right)\)

\(\Rightarrow x=\pm2\)

Vậy tập nghiệm của phương trình là: S = {2; -2}

a, \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\left(1\right)\\6x-5y=27\left(2\right)\end{matrix}\right.\)

Lấy (1) - (2) ta được : \(14y=-15-27=-42\Leftrightarrow y=-3\)

\(\Rightarrow6x-27=-15\Leftrightarrow6x=12\Leftrightarrow x=2\)

Vậy \(\left(x;y\right)=\left(2;-3\right)\)

b, \(3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow x=0;x=-\dfrac{4}{3}\)

c, \(x^4-3x^2-4=0\Leftrightarrow x^4+x^2-4x^2-4=0\)

\(\Leftrightarrow x^2\left(x^2-4\right)+x^2-4=0\Leftrightarrow\left(x^2+1\right)\left(x-2\right)\left(x+2\right)=0\)

\(\Leftrightarrow x=\pm2;x^2+1>0\)

Vậy nghiệm của phương trình là x = -2 ; x = 2 

Đặt t = x² – 2x. Khi đó,  phương trình đã cho trở thành:

2t² – 3t + 1 = 0  ⇔ [ t = 1 t = 1 2

* Với t= 1 thì x² – 2x = 1 hay x² – 2x – 1 =0 có ac < 0 nên phương trình này có 2 nghiệm.

* Với t = 1 2  thì x 2 - 2 x = 1 2 ⇔ x 2 - 2 x - 1 2 = 0  có ac < 0 nên phương trình này có 2 nghiệm.

Do đó, phương trình đã cho có 4 nghiệm.

Chọn D.