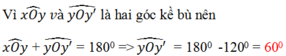cho hai góc kề bù xOy;yOy' .biết góc xOy bằng 1/5 góc yOy'.tính số đo các góc xOy và yOy'

Những câu hỏi liên quan
cho
cho góc xoy=30 độ . biết x'oy và xoy là hai góc kề bù x'oy' và y'oy là hai góc kề bù . số đo x'oy' la ?
em hoc lop sau nhung da co cau nay co giao giao de kho qua
Đúng 0
Bình luận (0)
Với hai góc kề bù ta có định lý sau: Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
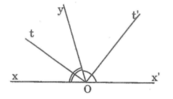
Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là mº.
A) cho góc mOn . Vẽ góc nOt kề bù với góc mOn . Vẽ góc mOz kề bù với góc mOn . Khiu đó mOn và tOz có phải là hai góc đối đỉnh ko?b)Cho góc hBk. vẽ Bm là tia phân giác của góc hBk . vẽ Bm là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. khi đó các góc mBj và hBm có phải là hai góc đối đỉnh koc)cho góc xOy vẽ góc yOz kề bù với góc xOy vẽ gos xOt kề bù với góc xOy. Vẽ Om kề bù với góc zOy vẽ Om là tia phân giác của góc tOxkhi đó zOn và xOm có phải là 2 góc đối đỉnh ko
Đọc tiếp
A) cho góc mOn . Vẽ góc nOt kề bù với góc mOn . Vẽ góc mOz kề bù với góc mOn . Khiu đó mOn và tOz có phải là hai góc đối đỉnh ko?
b)Cho góc hBk. vẽ Bm là tia phân giác của góc hBk . vẽ Bm' là tia đối của tia Bm. Vẽ góc kBj kề bù với góc hBk. khi đó các góc m'Bj và hBm có phải là hai góc đối đỉnh ko
c)cho góc xOy vẽ góc yOz kề bù với góc xOy vẽ gos xOt kề bù với góc xOy. Vẽ Om kề bù với góc zOy vẽ Om là tia phân giác của góc tOxkhi đó zOn và xOm có phải là 2 góc đối đỉnh ko
Ta có:
\(\widehat{mOz}\) kề bù với \(\widehat{mOn}\)
\(\widehat{nOt}\) kề bù với \(\widehat{mOn}\)
\(\Rightarrow\) \(\widehat{mOz}\) và \(\widehat{nOt}\) đối đỉnh
Đúng 0
Bình luận (0)
Cho hai góc kề bù xoy và yoz kề bù biết xoy-yoz=40
Tính số đo của xoy và yoz . vẽ hình minh họa
vì xoy và yoz là 2 góc kề bù =>xoz=180o
mà xoy-yoz=40o (dạng toán tổng hiệu)
xoy= (xoz+40o):2=(180+40):2=110o
yoz=180-110=70o
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hai góc kề bù góc xoy và góc yoz biết góc xoy = 80 độ, xoz = 30 độ
a) Gọi hai góc kề
\(\sqrt[]{\sqrt{ }\frac{ }{ }\hept{\begin{cases}\\\end{cases}}\hept{\begin{cases}\\\\\end{cases}}\orbr{\begin{cases}\\\end{cases}}^{ }^2_{ }|^{ }_{ }\sinh\le\chi}\)
Đúng 0
Bình luận (0)
cho góc xoy.vẽ góc yoz kề bù với góc xoy.vẽ góc xot kề bù với góc.a,góc xoy và góc zot có là hai góc đối đỉnh ko?b,giả sử góc xoy=35 độ,tính góc yoz,zot,xot
Cho góc xOy. Vẽ góc yOz kề bù với xOy. Vẽ góc xOt kề bù với góc xOy. Vẽ On là tia phân giác của góc zOy. Vẽ Om là tia phân giác của góc tOx. Khi đó zOn và xOm có phải là hai góc đối đỉnh không?
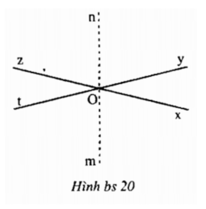
Vì góc yOz kề bù với góc xOy nên Oz là tia đối của tia Ox. Tương tự, góc xOt kề bù với góc xOy nên Ot là tia đối của tia Oy. Từ đó, hai góc zOy và tOx là hai góc đối đỉnh nên ∠zOy = ∠tOx.
Vì On, Om lần lượt là tia phân giác của góc zOy, góc xOt và ∠zOy = ∠tOx nên ∠zOn = ∠nOy = ∠xOm = ∠mOt.
Lại vì ∠zOn + ∠nOx = 180°,
Nên ∠mOx + ∠nOx = 180° hay ∠mOn = 180º.
Suy ra Om và On là hai tia đối nhau.
Từ đó, hai góc ∠zOn và ∠mOx là hai góc đối đỉnh.
Đúng 0
Bình luận (0)
Quan sát Hình 15 và giải thích vì sao:
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\) và \(\widehat {xOy} = \widehat {zOt}\)
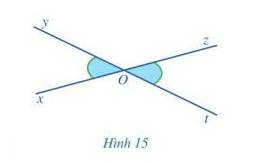
a) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.
Vậy hai góc xOy và yOz là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz là hai tia đối nhau nên hai góc xOy và yOz là hai góc kề bù.
b) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.
Vậy hai góc yOz và zOt là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot là hai tia đối nhau nên hai góc yOz và zOt là hai góc kề bù.
c) Do
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = 180^\circ ;\\\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 180^\circ \end{array}\)
Vậy \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\)
\( \Rightarrow \widehat {xOy} = \widehat {zOt}\)
Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.
Đúng 0
Bình luận (0)
cho góc xoy và góc yoz là hai góc kề bù tính xoy biết yoz=1/5 xoy
vì xOy và yOz là hai góc kề bù
=> xOy + yOz = 180 độ
Mà yOz = 1/5 xOy
Thay vào , ta được :
xOy + 1/5 xOy = 180 độ
xOy . ( 1 + 1/5 ) = 180 độ
xOy . 6/5 = 180 độ
xOy = 180 độ : 6/5
xOy = 150
Đúng 1
Bình luận (0)
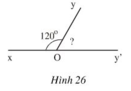
Hình 26 cho biết hai góc kề bù xOy và yOy', xOy = 120o. Tính góc yOy'.