Cho tứ diện ABCD. M,N lần lượt là trung điểm của AD và BD; G là trọng tâm tam giác ABC.
a) Tìm giao tuyến của mặt phẳng (ABC) và (MNG);
b) Xác định thiết diện tạo bởi (MNG) và tứ diện ABCD.
Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
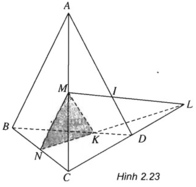
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.
Gọi L = NK ∩ CD
Ta có L ∈ NK ⇒ L ∈ (MNK)
L ∈ CD ⇒ L ∈ (ACD)
Nên ML = (ACD) ∩ (MNK) = Δ
Δ ∩ AD = I ⇒ I = (MNK) ∩ AD
Cho tứ diện ABCD có AC = 3a, B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
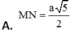
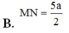
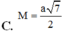
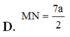
Cho tứ diện ABCD có A C = 3 a , B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.
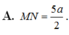
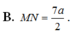
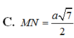

Cho tứ diện ABCD có AC=3a, BD=4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
A. M N = 5 a 2
B. M N = 7 a 2
C. M N = 7 a 2
D. M N = 5 a 2
Cho tứ diện ABCD có AC = 3a, BD = 4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
A. M N = a 5 2
B. M N = 5 a 2
C. M N = a 7 2
D. M N = 7 a 2
Phương pháp
+) Gọi P là trung điểm của AB. Chứng minh tam giác MNP vuông tại P.
+) Áp dụng định lý Pytago trong tam giác vuông MNP tính MN.
Cách giải

Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK) ?
Cho tứ diện ABCD, M là điểm thuộc BC sao cho MC = 2MB. N, P lần lượt là trung điểm của BD và AD. Điểm Q là giao điểm của AC với (MNP). Tính QA/QC.
A. Q A Q C = 1 2
B. Q A Q C = 2
C. Q A Q C = 2 3
D. Q A Q C = 3 2
NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
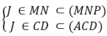
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
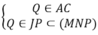
⇒ Q = AC ∩ (MNP). Có:
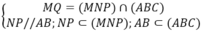
⇒MQ // NP // AB
Theo định lí Ta – lét có
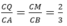
Kết luận:
Đáp án A
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
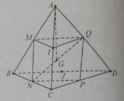
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Ta có N là trung điểm của BC
Suy ra A B → + A C → = 2 A N →
Lại có: A D → = 2 A Q → (Q là trung điểm của AD)
Do đó A B → + A C → + A D → = 2 A N → + 2 A Q → = 2 A N → + A Q → (1)
Tạ lại có G là trọng tâm của tứ diện ABCD nên G là trung điểm của NQ (tính chất trọng tâm của tứ diện) ⇒ A N → + A Q → = 2 A G → (2)
Từ (1) và (2) suy ra A B → + A C → + A D → = 4 A G → .
Đáp án A
Cho khối tứ diện đều ABCD có thể tích V, M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối tứ diện AMNPQ là:
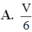
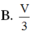
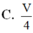
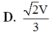
Cho khối tứ diện đều ABCD có thể tích V, M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối tứ diện AMNPQ là
A. V 6
B. V 3
C. V 4
D. 2 V 3