Cho góc xAy và đường tròn (o) tiếp xúc với Ax và Ay tại B và C trên đoạn thẳng BC lấy điểm M ( M # B và C ) . Đường thẳng vuông góc với OM tại M cắt Ax,Ay lần lược tại D và E . Chứng minh các điểm A,D,O,E nằm trên một đường tròn

Những câu hỏi liên quan
Cho góc xAy = 60 độ, đường tròn (O) tiếp xúc với tia Ax tại B, tiếp xúc với tia Ay tại C. Trên cung nhỏ BC của đường tròn (O) lấy điểm M, gọi D, E, F lần lượt là hình chiếu của điểm M trên BC, CA, AB. a. Chứng minh CDME là tứ giác nội tiếp b. Tính số đo góc EDF c. Chứng minh rằng MD^2= ME*MF
a: góc CEM+góc CDM=180 độ
=>CEMD nội tiếp
b: góc EDM=góc ECM
góc FDM=góc FBM=góc ABM
=>góc EDF=góc ACM+góc ABM=60 độ
Đúng 0
Bình luận (0)
Cho góc xAy = 60 độ, đường tròn (O)
tiếp xúc với tia Ax tại B, tiếp xúc với tia Ay tại C. Trên cung nhỏ BC của đường tròn (O) lấy điểm M, gọi D, E, F lần lượt là hình chiếu của điểm M trên BC, CA, AB.
a. Chứng minh CDME là tứ giác nội tiếp
b. Tính số đo góc EDF
c. Chứng minh rằng MD^2= ME*MF
a/
D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp
b/
CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp
\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)
Xét tứ giác nt CDME có
\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)
Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)
Xét \(\Delta ABC\) có
AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)
=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)
Ta có
\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\)
=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)
Ta có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\) cung BM (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)
\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)
c/
Xét tg vuông MBF và tg vuông MCD có
\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)
\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)
CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD
\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)
\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)
Đúng 1
Bình luận (0)
Mọi người giúp toy với =((( . ý b thoy ạ . Thanks with love
Cho góc xAy bằng 60 độ và (O) là đường tròn tiếp xúc với tia Ax tại B và tiếp xúc với tia Ay tại C. Trên cung nhỏ BC của đường tròn (O) lấy điểm M và gọi D, E, F lát lượt là hình chiếu vuông góc với M trên BC, CA, AB. a) Chứng minh tứ giác CDME là tứ giác nội tiếp. b) Tính số đo góc EDF. c) Chứng minh rằng MD bình = ME.MF
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
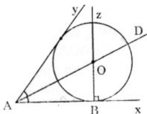
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy
Đúng 0
Bình luận (0)
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
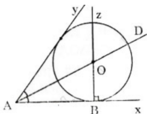
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. (Xem lại Bài 28 trang 116 SGK Toán 9 Tập 1) . Do đó ta có cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.
Đúng 0
Bình luận (0)
Cho 2 đường tròn (O;3cm) và (O'1cm) tiếp xúc ngoài tại A, 1 góc vuông xAy quay quanh A: Ax cắt (O)={B}; Ay cắt (O')= {C}
a) c/m OB //O'C và các tiếp tuyến ở B và C ở mỗi đường tròn // với nhau
b) BC cắt OO'={I}. c/m I cố định
c) Cho BC = 6cm. Tính IB, IC
Cho 2 đường tròn (O;3cm) và (O'1cm) tiếp xúc ngoài tại A, 1 góc vuông xAy quay quanh A: Ax cắt (O)={B}; Ay cắt (O')= {C}
a) c/m OB //O'C và các tiếp tuyến ở B và C ở mỗi đường tròn // với nhau
b) BC cắt OO'={I}. c/m I cố định
c) Cho BC = 6cm. Tính IB, IC
Cho 2 đường tròn (O;3cm) và (O'1cm) tiếp xúc ngoài tại A, 1 góc vuông xAy quay quanh A: Ax cắt (O)={B}; Ay cắt (O')= {C}
a) c/m OB //O'C và các tiếp tuyến ở B và C ở mỗi đường tròn // với nhau
b) BC cắt OO'={I}. c/m I cố định
c) Cho BC = 6cm. Tính IB, IC
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay ?

Cách dựng:
– Dựng tia phân giác At của góc xAy
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.
Đúng 0
Bình luận (0)












