Cho tam giác vuông ABC vuông góc tại A. Có cạnh AB dài 6cm, cạnh AC dài 8cm. Tính độ dài cạnh BC.

Những câu hỏi liên quan
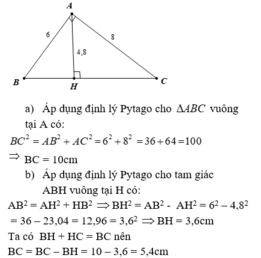
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. a) Tính độ dài cạnh BC. b)Kẻ AH vuông góc BC. Biết AH = 4,8cm. Tính độ dài các đoạn BH, CH .
Bài 7: Cho tam giác ABC vuông tại A (AB AC). BK là tia phân giác của góc ABC, K thuộc cạnh AC. Kẻ KI vuông góc với BC tại I. a) Tính độ dài cạnh BC biết AB 6cm; AC 8cm. b) Chứng minh 2 tam giác ABK IBK . Từ đó suy ra KA KI. c) Kẻ AD vuông góc với BC. Chứng minh: AI là tia phân giác của góc DAK. d) Gọi H là giao điểm của BK và AD. Chứng minh: HB + HC AB + AC. Giúp mình với!
Đọc tiếp
Bài 7: Cho tam giác ABC vuông tại A (AB < AC). BK là tia phân giác của góc ABC, K thuộc cạnh AC. Kẻ KI vuông góc với BC tại I.
a) Tính độ dài cạnh BC biết AB = 6cm; AC = 8cm.
b) Chứng minh 2 tam giác ABK = IBK . Từ đó suy ra KA = KI.
c) Kẻ AD vuông góc với BC. Chứng minh: AI là tia phân giác của góc DAK.
d) Gọi H là giao điểm của BK và AD. Chứng minh: HB + HC < AB + AC.
Giúp mình với!
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAK vuông tại A và ΔBIK vuông tại I có
BK chung
góc ABK=góc IBK
=>ΔBAK=ΔBIK
=>KA=KI
c: góc DAI+góc BIA=90 độ
góc CAI+góc BAI=90 độ
mà góc BIA=góc BAI
nên góc DAI=góc CAI
=>AI là phân giác của góc DAC
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC vuông tại A. Biết độ dài ba cạnh là: AB=6cm, AC=8cm và BC=10cm. Tính chiều cao tương ứng với cạnh đáy BC
Gọi AH là cc tương ứng với BC
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có cạnh AB=6cm,AC=8cm. Kẻ AH vuông góc với BC tại H. Khi đó độ dài của cạnh BH là.....cm
Giúp mình với ^^
B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
a. Tính độ dài cạnh BC
a. Áp dụng định lí Pytago trong tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100 ⇒ BC = 10cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm. Kẻ đường cao AH vuông góc với BC (H thuộc BC).
a) Tính độ dài BC.
b) Tia phản giác góc HAC cắt cạnh BC tại D. Qua D kẻ DK vuông góc với AC (K thuộc AC). Chứng minh: tam giác AHD = tam giác AKD.
c) Chứng minh: tam giác BAD cân.
d) Tia phân giác góc BAH cắt cạnh BC tại E. Chứng minh: AB+AC=BC+DE.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
b) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(cạnh huyền-góc nhọn)
Đúng 4
Bình luận (0)
c) Ta có: ΔADH vuông tại H(gt)
nên \(\widehat{HDA}+\widehat{HAD}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BDA}+\widehat{HAD}=90^0\)(2)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)(tia AD nằm giữa hai tia AB,AC)
nên \(\widehat{BAD}+\widehat{KAD}=90^0\)(3)
Từ (2) và (3) suy ra \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔBAD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔBAD cân tại B(Định lí đảo của tam giác cân)
Đúng 2
Bình luận (1)
Cho Tam giác ABC vuông tại A ,có AB=6cm,AC=8cm
a)Tính độ dài cạnh BC và chu vi hình tam giác ABC
b)Đường phân giác của góc B cắt AC tại D.Vẽ DH(vuông góc)B(H thuộc BC)
Chứng minh:tam giác ABD = HBD
c)Chứng minh DA <DC
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=6+8+10=24\left(cm\right)\)
Đúng 1
Bình luận (0)
b) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(Cạnh huyền-góc nhọn)
Đúng 0
Bình luận (0)
c) Ta có: ΔABD=ΔHBD(cmt)
nên DA=DH(hai cạnh tương ứng)
mà DH<DC(ΔDHC vuông tại H)
nên DA<DC
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc vuông tại a có các cạnh ab=6cm ac=8cm bc=10cm
a) tính diện tích tam giác abc
b) tính độ dài đường cao ah hạ từ đỉnh a xuống đáy bc
c) trên cạnh ab lấy điểm m sao cho ma=2mb. trên cạnh bc lấy điểm n sao cho nb=nc. kéo dài mn và ac cắt nhau tại p. tính độ dài đoạn cp
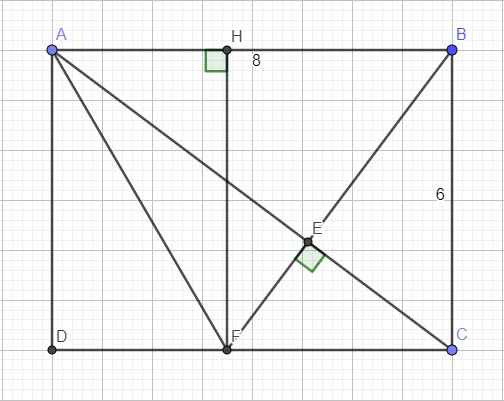
Cho hình chữ nhật ABCD có cạnh BC =6cm,AB =8cm. Đường thẳng kẻ từ B vuông góc với AC tại E , cắt cạnh AD tại F
a) Tính độ dài các đoạn thẳng AC,AE,BE
b)Tính độ dài các cạnh và diện tích tam giác ABF
Áp dụng định lý Pitago cho tam giác vuông ABC
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
Đúng 1
Bình luận (0)