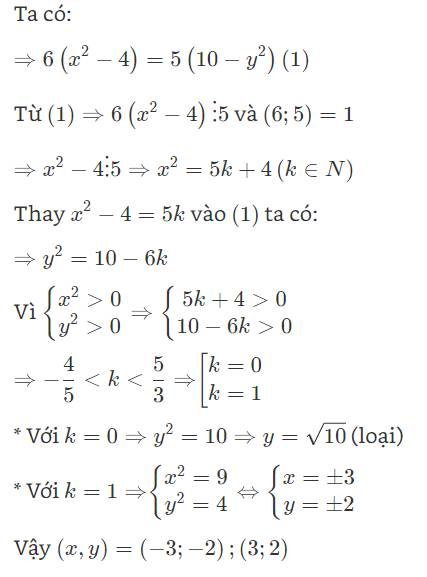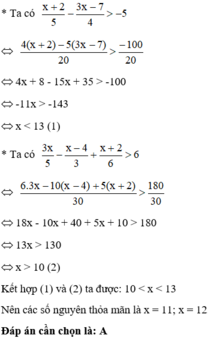Tìm số nguyên dương x biết:123-(-x)-25*4=74

Những câu hỏi liên quan
Bài 4: Tìm số nguyên x biết:
c) -62 + x = -14 + 46
d) 25 + ( x - 5 ) = -123 - ( 15 - 123 )
c: -62+x=-14+46
=>\(x-62=46-14=32\)
=>\(x=32+62=94\)
d: \(25+\left(x-5\right)=-123-\left(15-123\right)\)
=>\(x-5+25=-123-15+123\)
=>\(x+20=-15\)
=>\(x=-15-20=-35\)
Đúng 1
Bình luận (0)
`c) -62 + x = -14 + 46`
`-62 + x = 32`
`x = 32 - (-62)`
`x = 94`
Vậy `x = 94`
`d) 25 + ( x - 5 ) = -123 - ( 15 - 123 )`
`25 + ( x - 5 ) = -123 - 15 + 123`
`25 + ( x - 5 ) = - 15`
`x - 5 = -15 - 25`
`x - 5 = -40`
`x = -40 + 5`
`x = -35`
Vậy `x = -35`
Đúng 0
Bình luận (0)
Tìm số nguyên dương x,y biết 25 - y^3 = 8( x - 2021 )^2
tìm số nguyên dương nhỏ nhất x biết rằng: 12*x=25*y^2
1, tìm các số nguyên a, b, c biết rằng a+b=11, b+c=3 , c+a=2
2. tìm số nguyên x, biết
a, 25-/x/= 10
b, /x-2/+7 =12
c, x+4 là số nguyên dương nhỏ nhất
d, 10-x là số nguyên âm lớn nhất
Bài 2
a. 25-|x|=10
|x| =25-10
|x|=15
Vậy x=15 hoặc x=-15
sorry mk chưa làm được câu tiếp theo
b, |x-2|+7=12
|x-2| = 12-7
|x-2| = 5
+) Nếu x-2=5 thì x=7
+) Nếu x-2=-5 thì x=-3
Đúng 0
Bình luận (0)
bài 1 tìm số nguyên dương x y biết xy+4y-5y =25
Lời giải:
$xy+4y-5y=25$
$\Rightarrow xy-y=25$
$\Rightarrow y(x-1)=25$
Do $x,y$ là các số nguyên nên $y; x-1$ cũng là số nguyên.
Ta có các TH sau:
TH1: $y=1; x-1=25\Rightarrow y=1; x=26$
TH2: $y=-1; x-1=-25\Rightarrow y=-1; x=-24$
TH3: $y=5; x-1=5\Rightarrow y=5; x=6$
TH4: $y=-5; x-1=-5\Rightarrow y=-5; x=-4$
TH5: $y=25; x-1=1\Rightarrow y=25; x=2$
TH6: $y=-25; x-1=-1\Rightarrow y=-25; x=0$
Đúng 2
Bình luận (0)
Tìm x, biết: x.25 + x.75 = 31000.
Số giá trị nguyên dương của n thỏa mãn tích (n+5).(n+4).(n+3)...(n-3).(n-4).(n-5) = 0 là: (Nhập đáp án là số)
x.25+x.75=31000
x.(25+75)=31000
x.100=31000
x=31000:100
x=310
Trl :
Bạn kia làm đúng rồi nha!
Hok tốt
~ nha bạn ~
tìm các cặp số nguyên dương (x,y) thoả mãn : \(6x^2+5y^2=74\)
Cuu Cần gấp !!!!![]()
Tìm số nguyên thỏa mãn cả hai bất phương trình:
x
+
2
5
−
3x
−
7
4
−
5 và
3x
5
−
x
−
4
3
+
x
+
2
6
6
A. x 11; x 12 B. x 10; x 11 C. x -1...
Đọc tiếp
Tìm số nguyên thỏa mãn cả hai bất phương trình:
x + 2 5 − 3x − 7 4 > − 5 và 3x 5 − x − 4 3 + x + 2 6 > 6
A. x = 11; x = 12
B. x = 10; x = 11
C. x = -11; x = -12
D. x = 11; x = 12; x = 13
Tìm số nguyên dương x,y biết : 8(x-2005)2+y2-25=0
Vì \(x\)nguyên nên \(\left(x-2005\right)^2\)nguyên.
Nếu \(\left(x-2005\right)^2=0\Leftrightarrow x=2005\): phương trình ban đầu tương đương với:
\(y^2-25=0\Leftrightarrow y=\pm5\)
Nếu \(\left(x-2005\right)^2=1\Leftrightarrow\orbr{\begin{cases}x=2006\\x=2004\end{cases}}\), phương trình ban đầu tương đương với:
\(8+y^2-25=0\Leftrightarrow y=\pm\sqrt{17}\)(không thỏa mãn)
Nếu \(\left(x-2005\right)^2=2\Leftrightarrow x=2005\pm\sqrt{2}\)(loại)
Nếu \(\left(x-2005\right)^2=3\Leftrightarrow x=2005\pm\sqrt{3}\)(loại)
Nếu \(\left(x-2005\right)^2\ge4\):
\(y^2-25=-8\left(x-2005\right)^2\le-8.4=-32\Leftrightarrow y^2\le-7\)(vô nghiệm)
Vậy các cặp \(\left(x,y\right)\)thỏa mãn là: \(\left(2005,5\right);\left(2005,-5\right)\).