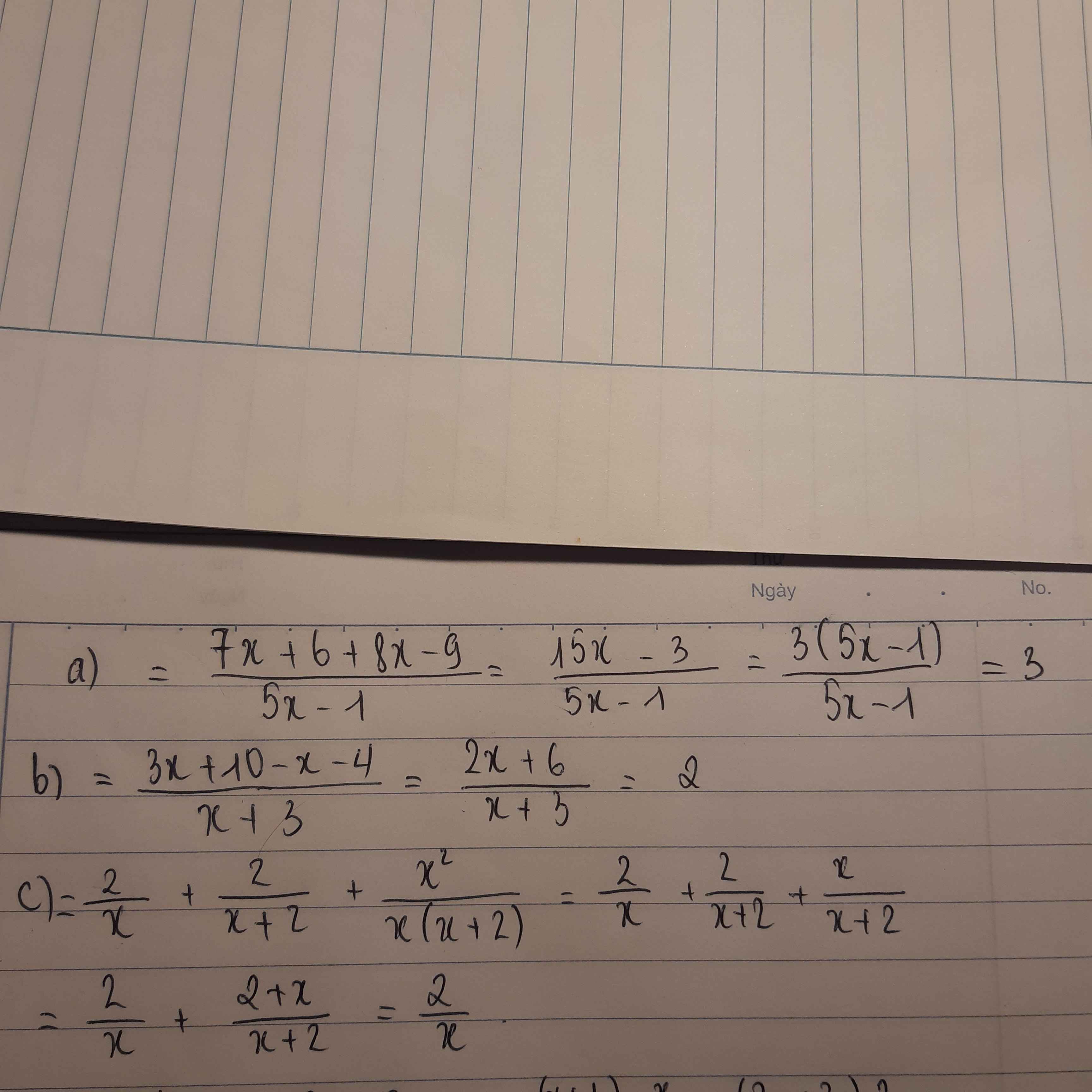Cho mik xin lời giải chi tiết vs ạ

Những câu hỏi liên quan
Mik xin lời giải chi tiết vs ạ

ai lm giúp mik vs ....mik đang cần gấp ạ ( cho mik lời giải chi tiết nhé ..cảm ơn)
Giúp mik vs ạ kèm lời giải chi tiết nha
1:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
=>AB//CD và AB=CD
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
=>ΔABC=ΔCDA
c: ΔCBA vuông tại A
mà AM là trung tuyến
nên AM=BC/2
Đúng 0
Bình luận (0)
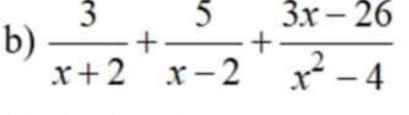 Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ
Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ
\(=\dfrac{3x-6+5x+10+3x-26}{\left(x-2\right)\left(x+2\right)}=\dfrac{11x-22}{\left(x-2\right)\left(x+2\right)}=\dfrac{11}{x+2}\)
Đúng 1
Bình luận (0)
Giúp mk lm bài hai ạ
Cho mk xin lời lời giải chi tiết ạ
Bài 1:
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
DO đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
Đúng 1
Bình luận (1)
Câu 1: Đĩa xích của xe đạp có 60 răng, đĩa líp có 30 răng. Tìm tỉ số truyền i và cho biết chi tiết nào quay nhanh hơn?
Ai lm giúp mik vs ạ ..Mik đang cần gấp ( Cho mik lời giải chi tiết nhé)
tham khảo
Z1= 60 răng
Z2= 30 răng
a) Ta có: i= Z1/Z2
=> i=60/30=2
b) đĩa líp quay nhanh hơn vì có số răng ít hơn đia xích
Đúng 1
Bình luận (0)
Cho em xin lời giải chi tiết ạ

Giúp mình với ạ cho mk xin lời giải chi tiết ạ
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
b: Xét ΔOEF có
OM là đường cao
OM là đường phân giác
Do đó: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của FE
hay FM=EM
Đúng 3
Bình luận (0)
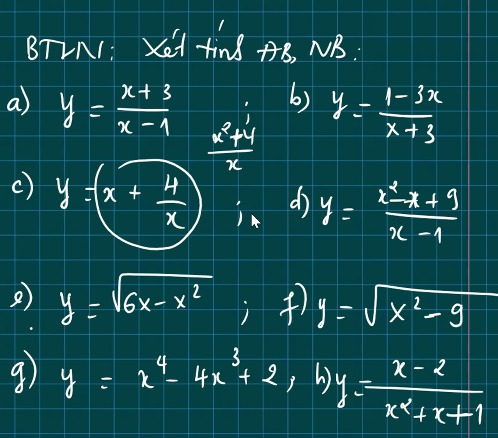 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ
f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
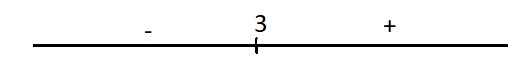
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
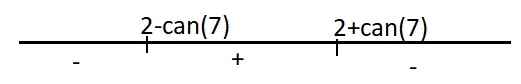
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)
Đúng 0
Bình luận (0)