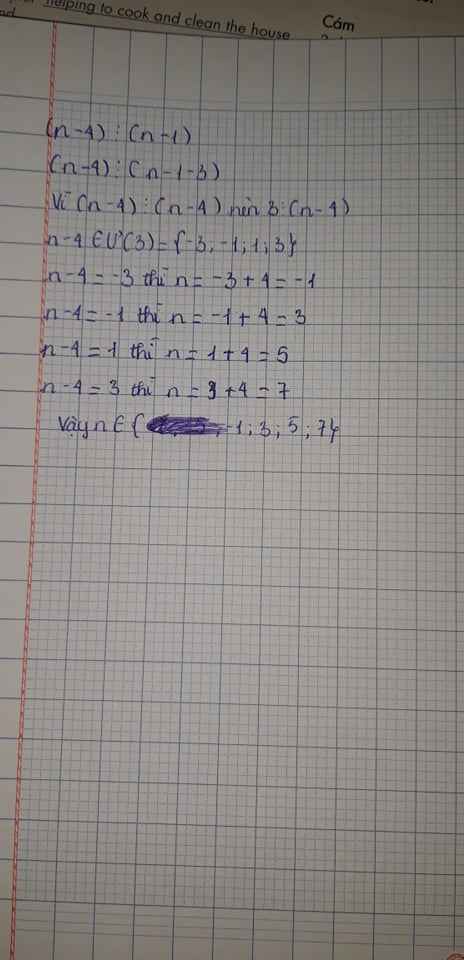░░░░░░███████ ]▄▄▄▄▄▄▄▃
▂▄▅█████████▅▄▃▂
I███████████████████].
◥⊙▲⊙▲⊙▲⊙▲⊙▲⊙▲⊙◤…

──────▄▌▐▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▌
───▄▄██▌█ ░Xe chở 100000000 đến đây..
▄▄▄▌▐██▌█ ░░░░░░ ░░░░░░░░░ ░░░░░░░▐\.
███████▌█▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄ ▄▄▌ \.
▀❍▀▀▀▀▀▀▀❍❍▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀❍❍ ▀▀.

                                hello

n²+13-13 chia hết cho n+3

=> n²-3²+3² chia het cho n+3

=> (n+3)(n-3)+9 chia het cho n+3

Vi (n+3)(n-3) chia het cho n+3 nen 9 chia het cho n+3

=> n+3 thuoc{+1;-1;+3;-3;+9;-9}

=> n thuoc {-2;-4;0;-6;6;-12}

n thuộc {-2;4;0;-6;6;-12}

Tìm n thuộc Z để n² +13n - 13 chia hết cho n + 3

Trả lời:

n² + 13 - 13 \(⋮\)n + 3

\(\Rightarrow\)n² - 3² + 3² \(⋮\)n + 3

\(\Rightarrow\)( n + 3 ) (  n - 3 ) + 9 \(⋮\)n + 3

Vì ( n + 3 ) (  n - 3 ) ​\(⋮\)chia hết cho n + 3 nên 9 \(⋮\)n + 3​

\(\Rightarrow n+3\in\left(+1;-1;+3;-3;+9;-9\right)\)

\(\Rightarrow n\in\left\{-2;-4;0;-6;6;-12\right\}\)

\(⋮\)

Ta có: n.(n + 13) - 13 chai hết n + 3

n.(n + 3) + 10n - 13 chia hết n + 3

=> 10.(n - 3) - 10 chia hết n + 3

=> 10.(n + 3 - 6) - 10 chia hết n + 3

=> 165

n^2 + 13n - 13 = n.n + 3n + 10n + 30 - 43 = n(n + 3) + 10(n + 3) - 43 
Vậy n^2 + 13n - 13 chia hết cho n+3 khi và chỉ khi n+3 là ước của 43 hay n+3 thuộc {-43; -1; 1; 43} 
---> n \(\in\) {-46; -4; -2; 40} 

\(n+3⋮2n+2\)

=>\(2n+6⋮2n+2\)

=>\(2n+2+4⋮2n+2\)

=>\(4⋮2n+2\)

=>\(2n+2\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(2n\in\left\{-1;-3;0;-4;2;-6\right\}\)

=>\(n\in\left\{-\dfrac{1}{2};-\dfrac{3}{2};0;-2;1;-3\right\}\)

mà n nguyên

nên \(n\in\left\{0;-2;1;-3\right\}\)

Ta có : n + 3 ⋮ 2n + 2 => 2(n + 3) = 2n + 6 ⋮ 2n + 2

=> (2n + 2) + 4 ⋮ 2n + 2

Vì 2n + 2 ⋮ 2n + 2 nên 4 ⋮ 2n + 2 => 2n + 2 ∈ Ư(4) ∈ {-4;-2;-1;1;2;4}

Mà 2n + 2 luôn chẵn => 2n + 2 ∈ -4;-2;2;4

=> n ∈ {-3;-2;0;1}

Mặt khác : n + 3 ⋮ 2n + 2 

=> n + 3 phải chẵn ( vì 2n + 2 chẵn)

=> n lẻ => n =-3;1

Ta có : n² + 13n - 13 = n² + (3n + n + 9n) + (3-16) = n² + 3n + n + 3 + 9n - 16 = n(n+3) + (n+3) + 9n -16

= (n+1)(n+3)+ 9n - 16.Vì (n+1)(n+3) chia hết cho n+3 nên để n²+13n-13 chia hết cho n+3 thì 9n-16 phải chia hết cho n+3.Ta lại có : 9n-16 = 9n+27-43 = 9(n+3) - 43.Vì 9(n+3) chia hết cho n+3 nên để 9n-16 chia hết cho n+3 thì 43 phải chia hết cho n+3 => n+3 = -43;-1;1;43 => n = -46;-4;-2;40

bai toan nay kho

n²+13n-13=n²+3n+10n+30-43 

=n.(n+3)+10.(n+3)-43

Để n²+13n-13 chia hết cho n+3 thì: 

n+3 thuộc U(43)={1;-1;43;-43}

=>n={-2;-4;40;-47}

Ta có :

để n^2+2 chia het cho n+2

=> n E {1}

GIÚP MIK với